题目内容
计算:
(1)-25+(
)-4+(π-3)0
(2)(5x2y3)2÷(25x4y5)
(3)-(-
)-2-(-1)2006+(
)11×(-
)12
(4)(x+2y)2-2(x-y)(x+y)+2y(x-3y)
(1)-25+(
| 1 |
| 2 |
(2)(5x2y3)2÷(25x4y5)
(3)-(-
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
(4)(x+2y)2-2(x-y)(x+y)+2y(x-3y)
考点:整式的混合运算
专题:计算题
分析:(1)原式第一平方差项利用乘方的意义化简,第二项利用负指数幂法则计算,最后一项利用零指数幂法则计算即可得到结果;
(2)原式先计算乘方运算,再计算除法运算即可得到结果;
(3)原式第一项利用负指数幂法则计算,第二项利用乘方的意义计算,第三项利用积的乘方逆运算法则变形,计算即可得到结果;
(4)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,最后一项利用单项式乘以多项式法则计算,去括号合并即可得到结果.
(2)原式先计算乘方运算,再计算除法运算即可得到结果;
(3)原式第一项利用负指数幂法则计算,第二项利用乘方的意义计算,第三项利用积的乘方逆运算法则变形,计算即可得到结果;
(4)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,最后一项利用单项式乘以多项式法则计算,去括号合并即可得到结果.
解答:解:(1)原式=-32+16+1=-15;
(2)原式=(25x4y6)÷(25x4y5)=y;
(3)原式=-16-1-
=-18
;
(4)原式=x2+4xy+4y2-2x2+2y2+2xy-6y2=-x2+6xy.
(2)原式=(25x4y6)÷(25x4y5)=y;
(3)原式=-16-1-
| 3 |
| 2 |
| 1 |
| 2 |
(4)原式=x2+4xy+4y2-2x2+2y2+2xy-6y2=-x2+6xy.
点评:此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
若关于x的一元二次方程(k-1)x2+2x-2=0有不相等实数根,则k的取值范围是( )
A、k>
| ||
B、k≥
| ||
C、k>
| ||
D、k≥
|
 已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF.
已知:如图,点A、B、C在同一直线上,AB=CD,AE∥CF,且AE=CF. 如图,一次函数y=ax+b与反比例函数y=
如图,一次函数y=ax+b与反比例函数y=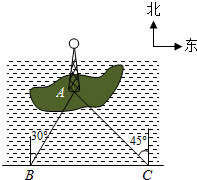 如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.
如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东30°的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西45°的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.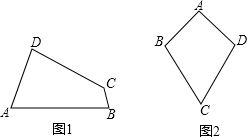 类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
类比梯形的定义,我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.