题目内容
6.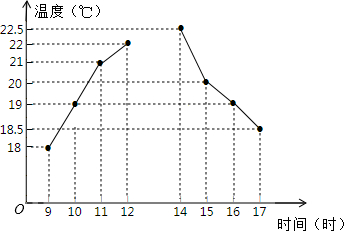 如图是小明根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图可知:该天下午(填上午或下午)的气温更稳定,理由是上午的方差大于下午的方差.
如图是小明根据杭州市某天上午和下午各四个整点时的气温绘制成的折线统计图.根据该统计图可知:该天下午(填上午或下午)的气温更稳定,理由是上午的方差大于下午的方差.
分析 方差就是各变量值与其均值离差平方的平均数,根据方差公式计算即可,所以计算方差前要先算出平均数,然后再利用方差公式计算.
解答 解:$\overline{x}$上=(18+19+21+22)÷4=20,
$\overline{x}$下=(22.5+20+19+18.5)÷4=20,
S上2=[(18-20)2+(19-20)2+(21-20)2+(22-20)2]÷4=2.5,
S下2=[(22.5-20)2+(20-20)2+(19-20)2+(18.5-20)2]÷4=2.375,
∵S上2>S下2,
∴下午的气温更稳定.
故答案为:下午;因为上午的方差大于下午的方差;
点评 此题主要考查了方差的计算方法,方差是各变量值与其平均值的差平方的平均数,它是测算数值型数据离散程度的最重要的方法.

练习册系列答案
相关题目
16.下列等式从左到右的变形,属于因式分解的是( )
| A. | m2+n2=(m+n)2 | B. | x2-1=x(x-$\frac{1}{x}$) | C. | a2-2a-1=(a-1)2-2 | D. | x2-4y2=(x-2y)(x+2y) |
17.下列计算正确的是( )
| A. | 2x+3x=6x2 | B. | 3x+4y=7xy | C. | 5x2-7x2=-2 | D. | 8x3y2-8y2x3=0 |
11.A、B两村生产雪花梨,A村有雪花梨200吨,B村有雪花梨300吨,现将这些雪花梨运动C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为40元/吨和45元/吨;从B村运往C、D两处的费用分别为25元/吨和32元/吨.设从A村运往C仓库的雪花梨为x吨,A、B两村往两仓库运雪花梨的运输费用分别为yA元、yB元.
(1)请填写下表,并求出yA、yB与x之间的函数关系式;
(2)当x为何值时,A村的运输费用比B村少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
(1)请填写下表,并求出yA、yB与x之间的函数关系式;
(2)当x为何值时,A村的运输费用比B村少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
| C | D | 总计 | |
| A | x吨 | 200-x吨 | 200吨 |
| B | 240-x吨 | 60+x吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
18.若单项式-3a5b与am+2b是同类项,则常数m的值为( )
| A. | -3 | B. | 4 | C. | 3 | D. | 2 |
16.9的平方根是( )
| A. | ±3 | B. | 3 | C. | -3 | D. | $\sqrt{9}$ |
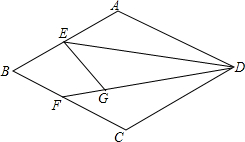 如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$.
如图,在菱形ABCD中,∠B=60°,E为AB的中点,将△AED沿DE翻折得到△GED,射线DG交BC于点F,若AD=2,则BF=$\frac{4}{5}$.