题目内容
完成下列各题:
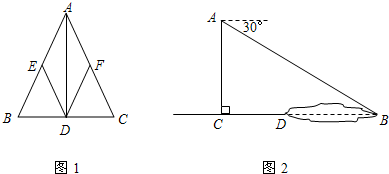
(1)如图1所示,在△ABC中,AD⊥BC于D,点D,E,F分别是BC,AB,AC的中点.求证:四边形AEDF是菱形.
(2)如图2所示,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取
≈1.73,结果保留整数)
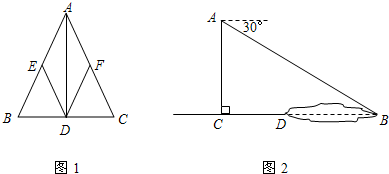
(1)如图1所示,在△ABC中,AD⊥BC于D,点D,E,F分别是BC,AB,AC的中点.求证:四边形AEDF是菱形.
(2)如图2所示,某同学在楼房的A处测得荷塘的一端B处的俯角为30°,荷塘另一端D与点C、B在同一直线上,已知AC=32米,CD=16米,求荷塘宽BD为多少米?(取
| 3 |
考点:菱形的判定,解直角三角形的应用-仰角俯角问题
专题:几何图形问题,证明题
分析:(1)首先判定四边形AEDF是平行四边形,然后证得AE=AF,利用邻边相等的平行四边形是菱形判定菱形即可;
(2)根据已知条件转化为直角三角形ABC中的有关量,然后选择合适的边角关系求得BD的长即可.
(2)根据已知条件转化为直角三角形ABC中的有关量,然后选择合适的边角关系求得BD的长即可.
解答:(1)证明:∵点D,E,F分别是BC,AB,AC的中点,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又∵AD⊥BC,BD=CD,
∴AB=AC,
∴AE=AF,
∴平行四边形AEDF是菱形;
(2)解:由题意知:∠CAB=60°,△ABC是直角三角形,
在Rt△ABC中,tan60°=
,
即
=
,
∴BC=32
米,
∴BD=32
-16≈39(米).
答:荷塘宽BD为39米.
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又∵AD⊥BC,BD=CD,
∴AB=AC,
∴AE=AF,
∴平行四边形AEDF是菱形;
(2)解:由题意知:∠CAB=60°,△ABC是直角三角形,
在Rt△ABC中,tan60°=
| BC |
| AC |
即
| BC |
| 32 |
| 3 |
∴BC=32
| 3 |
∴BD=32
| 3 |
答:荷塘宽BD为39米.
点评:本题考差了菱形的判定,解直角三角形的应用--仰角俯角问题.解(2)题的关键是利用仰俯角的定义将题目中的相关量转化为直角三角形ABC中的有关元素.

练习册系列答案
相关题目
下列各数中,是无理数的是( )
| A、-1.732 | ||
| B、1.414 | ||
C、
| ||
| D、3.14 |
 有一个数值转换器,原理如图,则当输入的x为144时,输出的y是( )
有一个数值转换器,原理如图,则当输入的x为144时,输出的y是( )| A、12 | ||
B、2
| ||
C、2
| ||
D、3
|
在实数0,-
,2,-
中最小的实数为( )
| 3 |
| 2 |
A、-
| ||
B、-
| ||
| C、2 | ||
| D、0 |

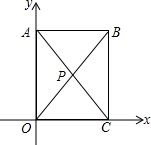 如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢?
如图,长方形ABCO对角线BO与AC的交点P到相对两边距离相等.若C点(2,0),P(1,2),请写出A,B坐标,你发现A,P,C三点横坐标有什么关系呢?纵坐标呢?