题目内容
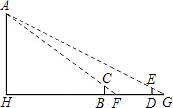 如图,要测量某建筑物的高度AB,立两根高为2m的标杆BC和DE,两竿相距BD=38m,D、B、H三点共线,从BC退行3m,到达点F,从点F看点A,A、C、F三点共线,从DE退行5m到达点G,从点G看点A,A、E、G三点也共线,试算出建筑物的高度AB及HB的长度.
如图,要测量某建筑物的高度AB,立两根高为2m的标杆BC和DE,两竿相距BD=38m,D、B、H三点共线,从BC退行3m,到达点F,从点F看点A,A、C、F三点共线,从DE退行5m到达点G,从点G看点A,A、E、G三点也共线,试算出建筑物的高度AB及HB的长度.考点:相似三角形的应用
专题:
分析:根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
解答:解:设BH=x,AH=y,根据题意可得:
BC∥AH,DE∥AH,
则△FCB∽△FAH,△EDG∽△AHG,
故
=
,
=
,
即
=
,
=
,
则
=
,
解得:x=57,
故
=
,
解得:y=40,
答:建筑物的高度AB为40m及HB的长度为57m.
BC∥AH,DE∥AH,
则△FCB∽△FAH,△EDG∽△AHG,
故
| BC |
| AH |
| BF |
| FH |
| DE |
| AH |
| DG |
| HG |
即
| 2 |
| y |
| 3 |
| 3+x |
| 2 |
| y |
| 5 |
| 5+38+x |
则
| 3 |
| 3+x |
| 5 |
| 5+38+x |
解得:x=57,
故
| 2 |
| y |
| 3 |
| 3+57 |
解得:y=40,
答:建筑物的高度AB为40m及HB的长度为57m.
点评:此题主要考查了相似三角形的判定与性质,得出△FCB∽△FAH,△EDG∽△AHG是解题关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 下列各选项这个的图形,与所给图形相似的是( )
下列各选项这个的图形,与所给图形相似的是( )A、 |
B、 |
C、 |
D、 |
 如图,
如图,