题目内容
在平面直角坐标系中,若一束光线从点A(0,2)发出,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为( )
A、
| ||
B、5
| ||
C、3
| ||
D、
|
考点:相似三角形的判定与性质,坐标与图形性质
专题:跨学科
分析:先过点B作BD⊥x轴于D,由A(0,2),B(5,3),即可得OA=2,BD=3,OD=5,由题意易证得△AOC∽△BDC,根据相似三角形的对应边成比例,即可得OA:BD=OC:DC=AC:BC=2:3,又由勾股定理即可求得这束光从点A到点B所经过的路径的长.
解答:解:如图,过点B作BD⊥x轴于D,
∵A(0,2),B(5,3),
∴OA=2,BD=3,OD=5,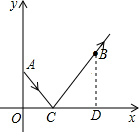
根据题意得:∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴OA:BD=OC:DC=AC:BC=2:3,
∴OC=5×
=2,
∴CD=OD-OC=3,
∴AC=
=2
,BC=
=3
,
∴AC+BC=5
,
故选B.
∵A(0,2),B(5,3),
∴OA=2,BD=3,OD=5,

根据题意得:∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴OA:BD=OC:DC=AC:BC=2:3,
∴OC=5×
| 2 |
| 5 |
∴CD=OD-OC=3,
∴AC=
| OA2+OC2 |
| 2 |
| BD2+CD2 |
| 2 |
∴AC+BC=5
| 2 |
故选B.
点评:此题考查了相似三角形的判定与性质、勾股定理以及点与坐标的性质.此题难度适中,解此题的关键是掌握辅助线的作法,掌握入射光线与反射光线的关系.

练习册系列答案
相关题目
已知a>b,则下列不等式中一定不正确的是( )
| A、a+5>b+5 | ||||
| B、3a>3b | ||||
| C、-5a>-5b | ||||
D、
|
 如图所示,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,若DC:DB=3:5,则点D到AB的距离是( )
如图所示,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,若DC:DB=3:5,则点D到AB的距离是( )| A、40 | B、15 | C、25 | D、20 |
 如图,等腰梯形ABCD中,AB∥CD,点E、F、G、H分别为各边中点,对角线AC=5,则四边形EFGH的周长为( )
如图,等腰梯形ABCD中,AB∥CD,点E、F、G、H分别为各边中点,对角线AC=5,则四边形EFGH的周长为( )| A、2.5 | B、5 | C、10 | D、20 |
在平面直角坐标系中,半径为1和6的两个圆的圆心坐标分别是(-3,0)和(0,4),则两圆的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
 如图,平行四边形ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交AD于点G,若AB=6,AD=8,则EG的长为
如图,平行四边形ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交AD于点G,若AB=6,AD=8,则EG的长为 如图,抛物线y=2x2-4x-1与y轴交于点A,其顶点是D,点A′的坐标是(2,2),将该抛物线沿AA′方向平移,使点A平移到点A′,则平移中该抛物线上A、D两点间的部分所扫过的面积是
如图,抛物线y=2x2-4x-1与y轴交于点A,其顶点是D,点A′的坐标是(2,2),将该抛物线沿AA′方向平移,使点A平移到点A′,则平移中该抛物线上A、D两点间的部分所扫过的面积是