题目内容
如果三角形的三边a、b、c适合a2(b-c)+b2(c-a)+c2(a-b)=0,那么△ABC的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
考点:因式分解的应用
专题:
分析:由原式通过因式分解得到(a-b)(c-a)(c-b)=0,由此可以求得a、b、c间的数量关系.
解答:解:原式=a2b-a2c+b2c-a22+c2(a-b)
=ab(a-b)-c(a+b)(a-b)+c2(a-b)
=(a-b)[c2-c(a+b)+ab]
=(a-b)(c-a)(c-b),
即(a-b)(c-a)(c-b)=0
所以a=b或c=a或c=b
故△ABC是等腰三角形.
故选B.
=ab(a-b)-c(a+b)(a-b)+c2(a-b)
=(a-b)[c2-c(a+b)+ab]
=(a-b)(c-a)(c-b),
即(a-b)(c-a)(c-b)=0
所以a=b或c=a或c=b
故△ABC是等腰三角形.
故选B.
点评:本题考查了因式分解的应用.注意由(a-b)(c-a)(c-b)=0推知a=b或c=a或c=b,但是也不一定a=b=c,所以该三角形是等腰三角形,也有可能是等边三角形,但是不一定是等边三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知M、N是线段AB的三等分点,C是BN的中点,CM=6cm,则AB为( )
| A、8cm | B、9cm |
| C、10cm | D、12cm |
已知点A(2,-3)关于y轴对称的是A′(a,b),则a+b的值是( )
| A、-5 | B、-1 | C、1 | D、5 |
不大于2009的正整数中是3的倍数但不是5的倍数的个数是( )
| A、536 | B、401 |
| C、133 | D、669 |
某市有7万名学生参加中考,要想了解这7万名学生的数学考试成绩,从中抽取了1000名考生的数学成绩进行分析,以下说法正确的是( )
| A、这1000名考生是总体的一个样本 |
| B、每名考生是个体 |
| C、7万名考生是总体 |
| D、7万名考生的数学成绩是总体 |
函数y=ax-3的图象与y=bx+4的图象交于x轴上一点,那么a:b等于( )
| A、-4:3 |
| B、4:3 |
| C、(-3):(-4) |
| D、3:(-4) |
若y与x成正比例,则y与x之间的关系是( )
| A、y=kx | ||
| B、y=kx(k≠0) | ||
C、y=
| ||
| D、无法确定 |
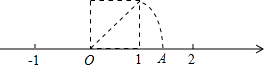 如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为圆心,正方形的对角线长为半径画弧,交数轴于点A,点A表示数x,则x2的平方根是( )
如图,以数轴的单位长线段为边作一个正方形,以数轴的原点为圆心,正方形的对角线长为半径画弧,交数轴于点A,点A表示数x,则x2的平方根是( ) 画出图中的物体的三种视图.
画出图中的物体的三种视图.