题目内容
11.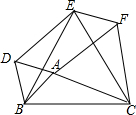 如图,以△ABC的三边AB、BC、CA分别为边,在BC的同侧作等边三角形ABD,BCE,CAF,求证:四边形ADEF是平行四边形.
如图,以△ABC的三边AB、BC、CA分别为边,在BC的同侧作等边三角形ABD,BCE,CAF,求证:四边形ADEF是平行四边形.
分析 由△ABD,△EBC都是等边三角形,易证得△DBE≌△ABC(SAS),则可得DE=AC,又由△ACF是等边三角形,即可得DE=AF,同理可证得AD=EF,即可判定四边形ADEF是平行四边形.
解答 证明:∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC
∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.
∴∠DBE=∠ABC.
在△DBE和△ABC中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBE=∠ABC}\\{BE=BC}\end{array}\right.$,
∴△DBE≌△ABC(SAS).
∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF.
∴DE=AF.
同理可证:AD=EF,
∴四边形ADEF是平行四边形.
点评 此题考查了平行四边形的判定、等边三角形的判定与性质以及全等三角形的判定与性质.注意证得△DBE≌△ABC≌△FEC是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
1.有下列说法:
①平行四边形具有四边形的所以性质
②平行四边形是中心对称图形
③平行四边形的对边相等
④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形
其中正确的有( )
①平行四边形具有四边形的所以性质
②平行四边形是中心对称图形
③平行四边形的对边相等
④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19. 如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )
如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )
 如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )
如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )| A. | S1=S2≠S3 | B. | S1=S3≠S2 | C. | S2=S3≠S1 | D. | S1=S2=S3 |
6.2016年春节黄金周海南旅游大幅增长,据统计,2月7至13日,全省共接待游客约3710000人次,将3710000用科学记数法表示为( )
| A. | 3.71×107 | B. | 0.371×107 | C. | 3.71×106 | D. | 37.1×106 |
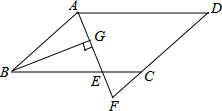 如图,在?ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为$\frac{34}{3}$.
如图,在?ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为$\frac{34}{3}$. 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s,同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s,同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题: 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.