题目内容
19. 如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )
如图,P,Q分别是双曲线y=$\frac{k}{x}$在第一、三象限上的点,PA⊥x轴,QB⊥y轴,垂足分别为A,B,点C是PQ与x轴的交点.设△PAB的面积为S1,△QAB的面积为S2,△QAC的面积为S3,则有( )| A. | S1=S2≠S3 | B. | S1=S3≠S2 | C. | S2=S3≠S1 | D. | S1=S2=S3 |
分析 根据题意可以证明△DBA和△DQP相似,从而可以求出S1,S2,S3的关系,本题得以解决.
解答 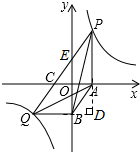 解:延长QB与PA的延长线交于点D,如右图所示,
解:延长QB与PA的延长线交于点D,如右图所示,
设点P的坐标为(a,b),点Q的坐标为(c,d),
∴DB=a,DQ=a-c,DA=-d,DP=b-d,
∵DB•DP=a•(b-d)=ab-ad=k-ad,
DA•DQ=-d(a-c)=-ad+cd=-ad+k=k-ad,
∴DB•DP=DA•DQ,
即$\frac{DB}{DQ}=\frac{DA}{DP}$,
∵∠ADB=∠PDQ,
∴△DBA∽△DQP,
∴AB∥PQ,
∴点B到PQ的距离等于点A到PQ的距离,
∴△PAB的面积等于△QAB的面积,
∵AB∥QC,AC∥BQ,
∴四边形ABQC是平行四边形,
∴AC=BQ,
∴△QAB的面积等于△QAC,
∴S1=S2=S3,
故选D.
点评 本题考查反比例函数系数k的几何意义、反比例函数的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
9.方程x2-3x-$\sqrt{{x}^{2}-3x+5}$=1根的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.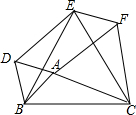 如图,以△ABC的三边AB、BC、CA分别为边,在BC的同侧作等边三角形ABD,BCE,CAF,求证:四边形ADEF是平行四边形.
如图,以△ABC的三边AB、BC、CA分别为边,在BC的同侧作等边三角形ABD,BCE,CAF,求证:四边形ADEF是平行四边形.