题目内容
在如图所示的3×3的方格中，画出2个面积小于9的不同的正方形，同时要求所画正方形的顶点都在方格的顶点上，并且写出边长（要求边长为无理数）
考点：勾股定理
专题：作图题
分析：根据题意画出图形，如图所示，求出面积，利用算术平方根的定义求出边长即可．
解答：解：根据题意得：
第一个图中，面积为5，边长为
；第二个图中，面积为2，边长
．
第一个图中，面积为5，边长为
| 5 |
| 2 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
下列因式分解正确的是（ ）
| A、4x2-1=（4x+1）（4x-1） |
| B、-m2+9=（m+3）（m-3） |
| C、x4-16=（x2-4）（x2+4） |
| D、4-（2m-n）2=（2+2m-n）（2-2m+n） |
下列各式正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列代数式的值中，一定是正数的是（ ）
| A、（x+1）2 |
| B、|x+1|+2 |
| C、（-x）2 |
| D、-x2+1 |
如图，已知在△ABC中，AB=AC，AD是BC边上的高，P是AB边上的一点，试在高AD上找一点E，使得△PEB的周长最短．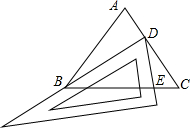
如图，在等边△ABC中，D是AC上一动点（与A、C不重合），使一块三角板的60°角的顶点与点D重合，并且斜边始终经过点B，一直角边与△ABC的边BC相交于点E．