Question

如图，已知菱形ABCD，E、F分别为AB、BC的中点，EP⊥DC，垂足为P，连接PF，若∠A=110°，则∠FPC=

 

．

Answer 1

考点：菱形的性质

专题：几何图形问题

分析：根据菱形的邻角互补求出∠B，再求出BE=BF，然后根据等腰三角形两底角相等求出∠BEF，再求出∠FEP，取AD的中点G，连接FG交EP于O，然后判断出FG垂直平分EP，再根据线段垂直平分线上的点到两端点的距离相等可得EF=FP，利用等边对等角求出∠FPE，再根据∠FPC=90°-∠FPE代入数据计算即可得解．

解答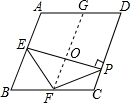：解：在菱形ABCD中，
∵∠A=110°，
∴∠B=180°-110°=70°，
∵E，F分别是边AB，BC的中点，
∴BE=BF，
∴∠BEF=

1

2

（180°-∠B）=

1

2

（180°-70°）=55°，
∵EP⊥CD，AB∥CD，
∴∠BEP=∠CPE=90°，
∴∠FEP=90°-55°=35°，
取AD的中点G，连接FG交EP于O，
∵点F是BC的中点，
∴FG垂直平分EP，
∴EF=PF，
∴∠FPE=∠FEP=35°，
∴∠FPC=90°-∠FPE=90°-35°=55°．
故答案为：55°．

点评：本题考查了菱形的性质，线段垂直平分线上的点到两端点的距离相等的性质，等边对等角的性质，熟记性质并作出辅助线求出EF=PF是解题的关键，也是本题的难点．