题目内容
16.已知$\frac{a}{4}$=$\frac{b}{5}$=$\frac{c}{6}$,且a-b+c=10,则a+b-c的值为6.分析 根据等比性质,可得$\frac{a}{4}$的值,再根据等式性质,可得答案.
解答 解:由等比性质,得
$\frac{a}{4}$=$\frac{a-b+c}{4-5+6}$=$\frac{10}{5}$=2,
$\frac{a}{4}$=$\frac{a+b-c}{4+5-6}$=2,
由等式的性质,得
a+b-c=2×3=6.
故答案为:6.
点评 本题考查了比例的性质,利用等比性质是解题关键,又利用了等式的性质.

练习册系列答案
相关题目
1.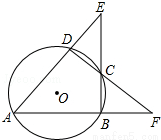 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
 如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )
如图,⊙O的内接四边形ABCD的两组对边的延长线分别交于点E、F,若∠E=α,∠F=β,则∠A等于( )| A. | α+β | B. | $\frac{α+β}{2}$ | C. | 180°-α-β | D. | $\frac{180°-α-β}{2}$ |
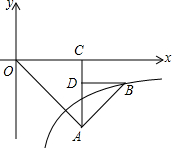 如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.
如图,△OAC和△BAD都是等腰直角三角形,反比例函数在第四象限经过点B,若OA2-AB2=8,则k的值为-4.