题目内容
12.阅读下列材料并解决有关问题:我们知道,|m|=$\left\{\begin{array}{l}{-m(m<0)}\\{0(m=0)}\\{m(m>0)}\end{array}\right.$.现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|m+1|+|m-2|时,可令m+1=0和m-2=0,分别求得m=-1,m=2(称-1,2分别为|m+1|与|m-2|的零点值).在实数范围内,零点值m=-1和m=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)m<-1;(2)-1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m-2|可分以下3种情况:
(1)当m<-1时,原式=-(m+1)-(m-2)=-2m+1;
(2)当-1≤m<2时,原式=m+1-(m-2)=3;
(3)当m≥2时,原式=m+1+m-2=2m-1.
综上讨论,原式=$\left\{\begin{array}{l}{-2m+1(m<-1)}\\{3(-1≤m<2)}\\{2m-1(m≥2)}\end{array}\right.$
通过以上阅读,请你解决以下问题:
(1)分别求出|x-5|和|x-4|的零点值;
(2)化简代数式|x-5|+|x-4|;
(3)求代数式|x-5|+|x-4|的最小值.
分析 (1)令x-5=0,x-4=0,解得x的值即可;
(2)分为x<4、4≤x<5、x≥5三种情况化简即可;
(3)根据(2)中的化简结果判断即可.
解答 (1)令x-5=0,x-4=0,
解得:x=5和x=4,
故|x-5|和|x-4|的零点值分别为5和4;
(2)当x<4时,原式=5-x+4-x=9-2x;
当4≤x<5时,原式=5-x+x-4=1;
当x≥5时,原式=x-5+x-4=2x-9.
综上讨论,原式=$\left\{\begin{array}{l}{9-2x(x<4)}\\{1(4≤x<5)}\\{2x-9(x≥5)}\end{array}\right.$.
(3)当x<4时,原式=9-2x>1;
当4≤x<5时,原式=1;
当x≥5时,原式=2x-9>1.
故代数式的最小值是1.
点评 本题主要考查的是绝对值的化简,根据例题进行解答是解题的关键.

练习册系列答案
相关题目
20.如果把分式$\frac{x+y}{2y}$中的x、y的值都扩大2倍,那么分式的值( )
| A. | 扩大2倍 | B. | 扩大6倍 | C. | 扩大3倍 | D. | 不变 |
1.设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的圆的圆心O在直线l上运动,A、O两点之间的距离为d.
(1)如图①,当r<a时,填表:
(2)如图②,⊙O与正方形有5个公共点B、C、D、E、F,求此时r与a之间的数量关系.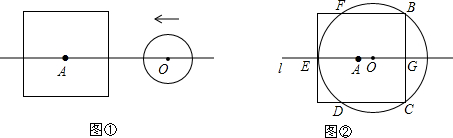
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
(1)如图①,当r<a时,填表:
| d,a,r之间的关系 | ⊙O与正方形的公共点个数 |
| d>a+r | 0 |
| d=a+r | 1 |
| a-r<d<a+r | 2 |
| d=a-r | 1 |
| 0≤d<a-r | 0 |
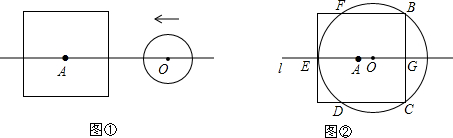
(3)由(1)可知,d、a、r之间的数量关系和⊙O的与正方形的公共点个数密切相关,当r=a时,请根据d、a、r之间的数量关系,判断⊙O与正方形的公共点个数.
(4)当r与a之间满足(2)中的数量关系,⊙O与正方形的公共点个数为0,1,2,5或8.
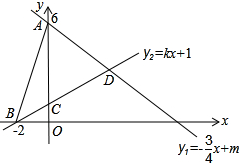 已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求:
已知如图,直线${l_1}:{y_1}=-\frac{3}{4}x+m$与y轴交于A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.求: