题目内容
若A(-1,y1)、B(-2,y2)是反比例函数y=
(m为常数,m≠
)图象上的两点,且y1>y2,则m的取值范围是 .
| 1-2m |
| x |
| 1 |
| 2 |
考点:反比例函数图象上点的坐标特征
专题:
分析:根据点A、B的坐标和y1>y2可以判定该双曲线在同一象限内y随x的增大而增大,则1-2m<0.由此可以求得m的取值范围.
解答:解:∵A(-1,y1)、B(-2,y2)是反比例函数y=
(m为常数,m≠
)图象上的两点,且y1>y2,
∴在双曲线y=
上,y随x的增大而增大,
∴1-2m<0,
解得 m>
故答案是:m>
.
| 1-2m |
| x |
| 1 |
| 2 |
∴在双曲线y=
| 1-2m |
| x |
∴1-2m<0,
解得 m>
| 1 |
| 2 |
故答案是:m>
| 1 |
| 2 |
点评:本题考查了反比例函数图象上点的坐标特征.此题利用反比例函数图象的增减性解题的.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列运算正确的是( )
| A、(-2x2)3=-8x5 |
| B、x2•x3=x6 |
| C、3a2-a2=3 |
| D、(3a-4b)(3a+4b)=9a2-16b2 |
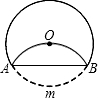 如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为
如图,⊙O的半径为6,将圆沿AB折叠后,圆弧恰好经过圆心,则弧AmB的长度为