题目内容
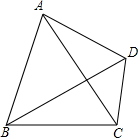如图所示，四边形ABCD中，∠BAD+∠BCD=180°，求证：∠BAC=∠BDC．考点：四点共圆
专题：证明题
分析：要证∠BAC=∠BDC，只需证明B、C、D、A四点共圆，可过B、C、D三点作圆，设该圆与直线AB相交于点A′，连接A′D，如图所示，只需证到点A与点A′重合即可．
解答：证明：过B、C、D三点作圆，与直线AB相交于点A′，连接A′D，如图所示，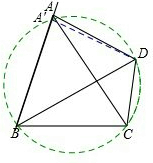
则B、C、D、A′四点共圆，
所以根据圆内接四边形的性质可得∠BA′D+∠BCD=180°．
∵∠BAD+∠BCD=180°，
∴∠BA′D=∠BAD，
∴点A与点A′重合，
∴B、C、D、A四点共圆，
∴根据圆周角定理可得∠BAC=∠BDC．
则B、C、D、A′四点共圆，
所以根据圆内接四边形的性质可得∠BA′D+∠BCD=180°．
∵∠BAD+∠BCD=180°，
∴∠BA′D=∠BAD，
∴点A与点A′重合，
∴B、C、D、A四点共圆，
∴根据圆周角定理可得∠BAC=∠BDC．
点评：本题着重考查了四点共圆、圆内接四边形的性质、圆周角定理等知识，运用同一法是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
方格纸上有A、B两点，若以B点为原点建立直角坐标系，则A点坐标为（-3，4），若以A点为原点建立直角坐标系，则B点坐标是（ ）
| A、（-3，-4） |
| B、（-3，4） |
| C、（3，-4） |
| D、（3，4） |
如图，∵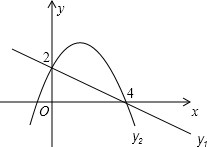
如图，已知直线y1=kx+n与抛物线y2=-x2+bx+c都经过A（4，0）和B（0，2）．