题目内容
如图：AB是圆O的直径，BD是圆O的弦，延长BD到C，AC=AB，求证：BD=CD．考点：圆周角定理,等腰三角形的性质
专题：证明题
分析：连结AD．先由直径所对的圆周角是直角得出∠ADB=90°，再根据等腰三角形三线合一的性质即可证明BD=CD．
解答：
证明：连结AD．
∵AB是圆O的直径，BD是圆O的弦，
∴∠ADB=90°，
∵AC=AB，
∴BD=CD．
证明：连结AD．∵AB是圆O的直径，BD是圆O的弦，
∴∠ADB=90°，
∵AC=AB，
∴BD=CD．
点评：本题考查了圆周角定理，等腰三角形的性质，根据圆周角定理得到∠ADB=90°是解题的关键．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
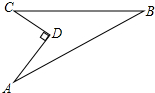如图所示，有一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，则这块地的面积．
如图，把△ABC的点A平移到点A1（-2，4），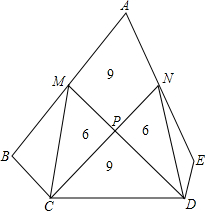
如图，在五边形ABCDE中，M、N分别是AB、AE的中点，四边形AMPN，