题目内容
3.有一函数y=a(x-1)5+bx+c.当x=2012时,函数值为1,并且b,c为整数,则当x=-2010时,函数值不可能为( )| A. | -5 | B. | 2 | C. | 1 | D. | 7 |
分析 根据有一函数y=a(x-1)5+bx+c.当x=2012时,函数值为1,代入函数解析式进行化简与x=-2010代入函数解析式可以建立关系,从而可以求得相应的函数值.
解答 解:∵有一函数y=a(x-1)5+bx+c.当x=2012时,函数值为1,
∴1=a(2012-1)5+b×2012+c=20115a+2012b+c,
∴-20115a=2012b+c+1,
∴当x=-2010时,y=a(-2010-1)5-2010b+c=-20115a-2010b+c=2012b+c+1-2010b+c=2b+2c+1=2(b+c)+1,
∵b,c为整数,
∴2(b+c)+1一定为奇数,
∴函数值不可能为2.
故选B.
点评 本题考查函数值,解题的关键是根据已知条件与所求的函数值建立关系.

练习册系列答案
相关题目
16.下列说法不正确的是( )
| A. | 有一个角等于60°的两个等腰三角形相似 | |
| B. | 有一个底角等于30°的两个等腰三角形相似 | |
| C. | 有一个锐角相等的两个等腰三角形相似 | |
| D. | 有一个锐角相等的两个直角三角形相似 |
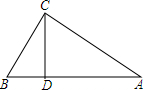 如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求:
如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求: ,求弦AE的长.
,求弦AE的长.