题目内容
18．
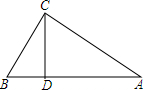如图，D为△ABC边AB上一点，且CD分△ABC为两个相似比为1：$\sqrt{3}$的一对相似三角形；（不妨如图假设左小右大），求：（1）△BCD与△ACD的面积比；
（2）△ABC的各内角度数．
分析 （1）根据相似三角形面积的比等于相似比的平方解答；
（2）根据锐角三角函数的概念解答即可．
解答 解：（1）∵△BCD和△CAD的相似比为1：$\sqrt{3}$，
∴△BCD和△CAD的面积比为1：3；
（2）∵△BCD∽△CAD，
∴∠BDC=∠ADC=90°，
tanA=$\frac{CD}{AD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∴∠A=30°，
tanB=$\frac{CD}{BD}$=$\sqrt{3}$，
∴∠B=60°，
∴∠ACB=90°．
点评 本题考查的是相似三角形的性质，掌握相似三角形面积的比等于相似比的平方以及锐角三角函数的概念是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（-2，6）的对应点A′的坐标是（6，2）．
李先生准备在永川某小区内购买一套小户型商品房，他去某楼盘了解情况得知，该户型商品房的单价是8000元/m2，面积如图所示（单位：m，卫生间的宽未定，设宽为xm），售房部为李先生提供了以下两种优惠方案：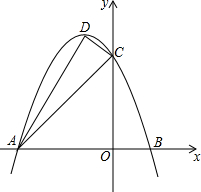
如图抛物线y=ax2+bx+3与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C，顶点为D，连接AC、CD、AD．
圆内接四边形ABCD，两组对边的延长线分别相交于点E、F，且∠E=40°，∠F=60°，求∠A=40°．