题目内容
8.已知A(-1,2)和B(-3,-2),试在y轴上确定一点P,使其到A、B的距离和最小,求P点的坐标.分析 作出B点关于y轴的对称点B′,连接AB′交y轴于点P,由两点之间线段最短可知,点P即为所求点,用待定系数法求出过AB′的一次函数解析式,再求出此函数与y轴的交点即可.
解答 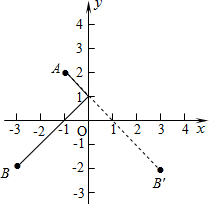 解:如图所示,作出B(-3,-2)关于y轴的对称点B′(3,-2),连接AB′交y轴于点P,
解:如图所示,作出B(-3,-2)关于y轴的对称点B′(3,-2),连接AB′交y轴于点P,
设过A、B′两点的一次函数解析式为y=kx+b(k≠0),
因为A(-1,2),B′(3,-2),
所以$\left\{\begin{array}{l}{2=-k+b}\\{-2=3k+b}\end{array}\right.$,
解得k=-1,b=1.
故此一次函数的解析式为:y=-x+1,当x=0时,y=1,故P点坐标为(0,1).
点评 本题考查的是轴对称-最短路线问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
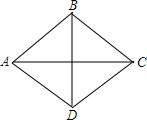 如图,菱形ABCD的边长为10,sin∠BAC=$\frac{3}{5}$,则对角线AC的长为16.
如图,菱形ABCD的边长为10,sin∠BAC=$\frac{3}{5}$,则对角线AC的长为16. ,其中
,其中 .
. 如图,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC长度.(tan15°=2-$\sqrt{3}$)
如图,在△ABC中,∠B=15°,∠C=60°,AC=2,求BC长度.(tan15°=2-$\sqrt{3}$)