题目内容
15.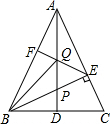 如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.
如图,在△ABC中,AB=AC,BE⊥AC于点E,BE=AE,AD是∠BAC的角平分线,和BE相交于点P,和BC边交于点D,点F是AB边的中点,连结EF,交AD于点Q,连结BQ.(1)求证:△BCE≌△APE;
(2)求证:BD=$\frac{1}{2}$AP;
(3)判断△BDQ的形状,并证明你的结论.
分析 (1)求出∠AEP=∠BEC=90°,根据三角形内角和定理求出∠EBC=∠EAP,根据ASA推出△BCE≌△APE即可;
(2)根据全等得出BC=AP,根据等腰三角形的性质得出BD=$\frac{1}{2}$BC,即可求出答案;
(3)根据线段垂直平分线的性质求出AQ=BQ,求出∠BAE=45°,根据角平分线的定义求出∠BAD=∠ABQ=22.5°,根据三角形外角性质求出∠BQD=45°,即可得出答案.
解答 证明:(1)如图:
∵AD是∠BAC的角平分线,AB=AC,
∴∠BDP=90°,BD=CD,
∵BE⊥AC,
∴∠AEP=∠BEC=90°,
∵在△BPD和△APE中,∠AEP=∠BDP=90°,∠BPD=∠APE,∠PAE+∠PEA+∠APE=180°,∠BDP+∠BPD+∠EBC=180°,
∴∠EBC=∠EAP,
在△BCE和△APE中,
$\left\{\begin{array}{l}{∠EBC=∠EAP}\\{BE=AE}\\{∠BEC=∠AEP}\end{array}\right.$,
∴△BCE≌△APE;
(2)∵△BCE≌△APE,
∴BC=AP,
∵BD=CD,
∴BD=$\frac{1}{2}$BC,
∴BD=$\frac{1}{2}$AP;
(3)△BDQ是等腰直角三角形,
证明:∵BE=AE,F是AB的中点,
∴EF是线段AB的垂直平分线,
∴AQ=BQ,
∴∠BAQ=∠ABQ,
∵BE=AE,∠BEA=90°,
∴∠BAE=45°,
∵AD是∠BAC的角平分线,
∴∠BAD=∠CAD=22.5°,
∵∠BAD=∠ABQ,
∴∠BAD=∠ABQ=22.5°,
∴∠BQD=22.5°×2=45°,
∵∠ADB=90°,
∴△BDQ是等腰直角三角形.
点评 本题考查了全等三角形的性质和判定,线段垂直平分线性质,等腰三角形的性质和判定,等腰直角三角形性质的应用,能综合运用定理进行推理是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.

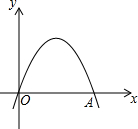 如图,已知抛物线的顶点在第一象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.
如图,已知抛物线的顶点在第一象限,顶点到x轴的距离为3,抛物线与x轴交于原点O(0,0)及点A,且OA=4.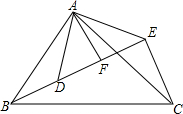 已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是BE=CE+2AF.
已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是BE=CE+2AF.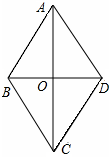 已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( )
已知:如图,菱形ABCD的四边相等,且对角线互相垂直平分.在菱形ABCD中,对角线AC、DB相交于点O,且AC≠BD,则图中全等三角形有( ) 如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.
如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.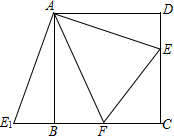 如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.
如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD的周长的一半.