Question

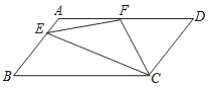
【题目】如图，在菱形中，，过点作于点，交对角线于点，过点作于点.

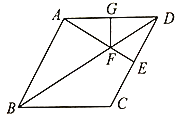
（1）若，求四边形的面积；（2）求证：.（温馨提示；连接）

Answer 1

【答案】（1）四边形的面积是；（2）见解析.

【解析】

(1)首先求出△ABD的面积,再求出RT△DFG的面积是，进而可求出四边形ABFG的面积是.

(2) 连结AC，交BD于点O，根据已知条件和菱形的性质看证明△ABO≌△DAE和△AOF≌△AGF，由全等三角形的性质即可证明BF=AE+FG

（1）∵∠1=∠2=30，

∴AF=DF.

又∵FG⊥AD于点G，

∴AG=AD，

∵AB=2，

∴AD=2，AG=1.

∴DG=1,AO=1,FG=,BD=，

∴△ABD的面积是,RT△DFG的面积是

∴四边形ABFG的面积是53√6.∴四边形的面积是.

（2）证明：连结交于点.

∵四边形ABCD是菱形，

∴AB=AD,∠ABC=∠ADC,∠4=12∠ABC,∠2=12∠ADC，AC⊥BD，

∵∠ABC=60，

∴∠2=∠4=12∠ABC=30，

又∵AE⊥CD于点E,

∴∠AED=90，

∴∠1=30，

∴∠1=∠4,∠AOB=∠DEA=90，

∴△ABO≌△DAE，

∴AE=BO.

又∵FG⊥AD于点G，

∴∠AOF=∠AGF=90，

又∵∠1=∠3，AF=AF，

∴△AOF≌△AGF，

∴FG=FO.

∴BF=AE+FG.