题目内容
3.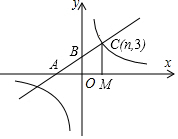 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=$\frac{m}{x}$(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=$\frac{3}{4}$,OA=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=$\frac{m}{x}$(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=$\frac{3}{4}$,OA=2.(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.
分析 (1)利用三角函数求得AM的长,则C的坐标即可求得,利用待定系数法求得反比例函数解析式,然后利用待定系数法求得一次函数的解析式;
(2)首先求得D的坐标,然后利用三角形的面积公式求解.
解答 解:(1)∵在直角△ACM中,tan∠CAM=$\frac{CM}{AM}$=$\frac{3}{4}$,CM=3,
∴AM=4,
∴OM=AM-OA=4-2=2.
∴n=2,
则C的坐标是(2,3).
把(2,3)代入y=$\frac{m}{x}$得m=6.
则反比例函数的解析式是y=$\frac{6}{x}$;
根据题意得$\left\{\begin{array}{l}{-2k+b=0}\\{2k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{y=\frac{3}{2}}\end{array}\right.$,
则一次函数的解析式是y=$\frac{3}{4}$x+$\frac{3}{2}$;
(2)在y=$\frac{6}{x}$中令y=-3,则x=-2.
则D的坐标是(-2,-3).
AD=3,
则S△ABD=$\frac{1}{2}$×3×2=3.
点评 本题考查了用待定系数法求出一次函数、反比例函数的解析式,一次函数与反比例函数的交点问题的应用,主要考查学生能否运用这些性质进行计算,本题具有一定的代表性,是一道不错的题目,数形结合思想的运用.

练习册系列答案
相关题目
19.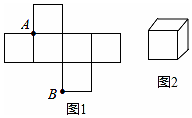 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )
如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A,B在围成的正方体上的距离是( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
20.调查显示,“两会”期间,通过手机等移动端设备对“两会”相关话题的浏览量高达115 000 000次.将115 000 000 用科学记数法表示应为( )
| A. | 1.15×109 | B. | 11.5×107 | C. | 1.15×108 | D. | 1.158 |
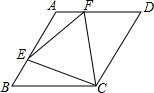 如图,菱形ABCD中,∠B=60°,AB=2,点E、F分别是AB、AD上的动点,且满足BE=AF,接连EF、EC、CF.求证:△EFC是等边三角形.
如图,菱形ABCD中,∠B=60°,AB=2,点E、F分别是AB、AD上的动点,且满足BE=AF,接连EF、EC、CF.求证:△EFC是等边三角形.