题目内容
9. 如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )
如图,将长方形ABCD沿直线BD折叠,使点C落在点E处,BE交AD于F,连接CE,下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD,正确的是( )| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
分析 根据折叠的性质、全等三角形的判定和性质、圆心角、弦、弧之间的关系定理判断即可.
解答 解:由折叠的性质可知,DE=DC,∠BED=∠BCD=90°,
在△ABF和△EDF中,
$\left\{\begin{array}{l}{∠AFB=∠EFD}\\{∠A=∠DEF}\\{AB=ED}\end{array}\right.$,
∴△ABF≌△EDF,
∴FA=FE,①正确;
由折叠的性质可知,∠EBD=∠CBD,
∴BD平分∠FBC,②正确;
∵∠BED=∠BCD=90°,
∴E、B、C、D四点共圆,又DE=DC,
∴∠DEC=∠EBD,③正确;
由折叠的性质可知,BD垂直平分EC,④错误,
故选B.
点评 本题考查的是翻转变换的性质,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
9.下列说法正确的是( )
| A. | 一个数的绝对值一定比0大 | B. | 倒数等于它本身的数是±1 | ||
| C. | 绝对值等于它本身的数一定是正数 | D. | 一个数的相反数一定比它本身小 |
7.如果零上2℃记作+2℃,那么零下3℃记作( )
| A. | 3 | B. | -3 | C. | -3℃ | D. | +3℃ |
 如图所示,现有两道互相垂直的墙,墙的东西方向长10米、南北方向长6米.张大爷想利用这两道墙围出一个面积为24平方米的矩形牛栏ABCD,牛栏的两边利用墙,另两边用长11米的篱笆围起来,问牛栏东西方向的长BC为多少米?
如图所示,现有两道互相垂直的墙,墙的东西方向长10米、南北方向长6米.张大爷想利用这两道墙围出一个面积为24平方米的矩形牛栏ABCD,牛栏的两边利用墙,另两边用长11米的篱笆围起来,问牛栏东西方向的长BC为多少米?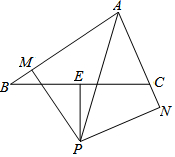 如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.
如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.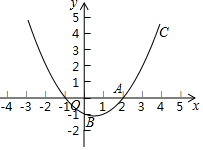 如图,已知二次函数y=ax2+bx+c的图象经过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象经过A(2,0),B(0,-1)和C(4,5)三点.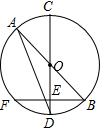 已知直径CD⊥弦BF于 E,AB为?O的直径.
已知直径CD⊥弦BF于 E,AB为?O的直径. 如图,一农户要建一个矩形鸡舍,为了节省材料鸡舍的一边利用长为12米的墙,另外三边用长为25米的建筑材料围成,为方便进出,在垂直墙的一边留下一个宽1米的门,所围成矩形鸡舍的长、宽分别是多少时,鸡舍面积为80平方米?
如图,一农户要建一个矩形鸡舍,为了节省材料鸡舍的一边利用长为12米的墙,另外三边用长为25米的建筑材料围成,为方便进出,在垂直墙的一边留下一个宽1米的门,所围成矩形鸡舍的长、宽分别是多少时,鸡舍面积为80平方米?