题目内容
把下列各个式子因式分解:
(1)a2-4ab+4b2-6a+12b-7;
(2)16-(x2-4x+2)2;
(3)x2-x-1;
(4)4x4-13x2+9.
(1)a2-4ab+4b2-6a+12b-7;
(2)16-(x2-4x+2)2;
(3)x2-x-1;
(4)4x4-13x2+9.
考点:因式分解-十字相乘法等,因式分解-分组分解法,实数范围内分解因式
专题:
分析:(1)首先将前三项分组,进而利用完全平方公式以及十字相乘法分解因式得出即可;
(2)首先利用平方差公式分解因式进而利用实数范围内分解因式的方法分解即可;
(3)首先求出x2-x-1=0的根进而分解因式得出即可;
(4)首先利用平方差公式分解因式,再利用十字相乘法分解因式得出即可.
(2)首先利用平方差公式分解因式进而利用实数范围内分解因式的方法分解即可;
(3)首先求出x2-x-1=0的根进而分解因式得出即可;
(4)首先利用平方差公式分解因式,再利用十字相乘法分解因式得出即可.
解答:解:(1)a2-4ab+4b2-6a+12b-7
=(a-2b)2-6(a-2b)-7
=(a-2b-7)(a-2b+1);
(2)16-(x2-4x+2)2
=42-(x2-4x+2)2,
=(4+x2-4x+2)(4-x2+4x-2)
=-(x2-4x+6)(x-2-
)(x-2+
);
(3)当x2-x-1=0,
解得:x1=
,x2=
,
故原式=(x-
)(x-
);
(4)4x4-13x2+9
=(x2-1)(4x2-9)
=(x+1)(x-1)(2x+3)(2x-3).
=(a-2b)2-6(a-2b)-7
=(a-2b-7)(a-2b+1);
(2)16-(x2-4x+2)2
=42-(x2-4x+2)2,
=(4+x2-4x+2)(4-x2+4x-2)
=-(x2-4x+6)(x-2-
| 5 |
| 5 |
(3)当x2-x-1=0,
解得:x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
故原式=(x-
1+
| ||
| 2 |
1-
| ||
| 2 |
(4)4x4-13x2+9
=(x2-1)(4x2-9)
=(x+1)(x-1)(2x+3)(2x-3).
点评:此题主要考查了实属范围内分解因式以及公式法分解因式,熟练利用十字相乘法分解因式是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
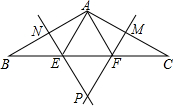 如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中:
如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中: