题目内容
已知x2+x-1=0,求x(1-
)÷(x+1)-
的值.
| 2 |
| 1-x |
| (x2-1) |
| x2-2x+1 |
考点:分式的化简求值
专题:
分析:先化简所给的代数式,然后解所给的方程,灵活运用解求值即可.
解答:解:x(1-
)÷(x+1)-
=x×
×
-
=-x×
×
-
=-
-
=
-
=-
=
,
解方程x2+x-1=0,得
x1=
,x2=
,
∴x2=
,
=
∵x2+x-1=0,
∴1-x=x2,
∴原式=
=
=
或
.
| 2 |
| 1-x |
| (x2-1) |
| x2-2x+1 |
=x×
| 1-x-2 |
| 1-x |
| 1 |
| x+1 |
| (x+1)(x-1) |
| (x-1)2 |
=-x×
| 1+x |
| 1-x |
| 1 |
| 1+x |
| x+1 |
| x-1 |
=-
| x |
| 1-x |
| x+1 |
| x-1 |
=
| x |
| x-1 |
| x+1 |
| x-1 |
=-
| 1 |
| x-1 |
=
| 1 |
| 1-x |
解方程x2+x-1=0,得
x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴x2=
3±
| ||
| 2 |
| 1 |
| x2 |
3±
| ||
| 2 |
∵x2+x-1=0,
∴1-x=x2,
∴原式=
| 1 |
| 1-x |
=
| 1 |
| x2 |
=
3+
| ||
| 2 |
3-
| ||
| 2 |
点评:考查了分式的化简与求值问题:解题的关键是正确化简所给的分式,灵活变形求值.

练习册系列答案
相关题目
满足下列条件的△ABC,不是直角三角形的是( )
| A、b2=c2-a2 |
| B、a:b:c=3:4:6 |
| C、∠C=∠A+∠B |
| D、∠A:∠B:∠C=9:16:25 |
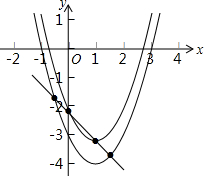 如图,抛物线c1:y=(x-1)2-
如图,抛物线c1:y=(x-1)2- 如图,AB=AC,AD=AE,求证:DE⊥BC.
如图,AB=AC,AD=AE,求证:DE⊥BC. 如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.
如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.