题目内容
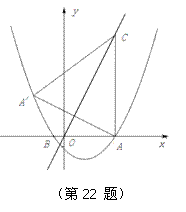
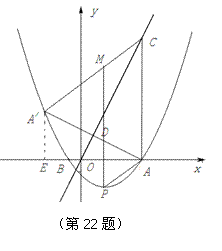
如图,抛物线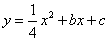 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x 轴,交直线
轴,交直线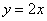 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线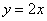 的对称点
的对称点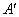 的坐标,判定点
的坐标,判定点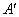 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段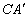 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵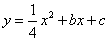 与x轴交于A(5,0)、B(-1,0)两点,
与x轴交于A(5,0)、B(-1,0)两点,
∴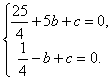 , 解得
, 解得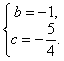
∴抛物线的解析式为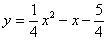
(2)过点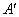 作
作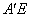 ⊥x轴于E,AA/与OC交于点D,
⊥x轴于E,AA/与OC交于点D,
∵点C在直线y=2x上, ∴C(5,10)
∵点A和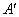 关于直线y=2x对称,
关于直线y=2x对称,
∴OC⊥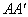 ,
,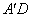 =AD.
=AD.
∵OA=5,AC=10,
∴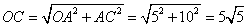 .
.
∵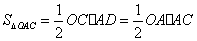 , ∴
, ∴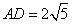 .∴
.∴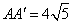 .
.
在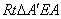 和Rt
和Rt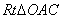 中,
中,
∵∠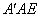 +∠
+∠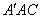 =90°,∠ACD+∠
=90°,∠ACD+∠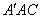 =90°,
=90°,
∴∠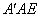 =∠ACD.
=∠ACD.
又∵∠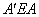 =∠OAC=90°,
=∠OAC=90°,
∴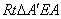 ∽
∽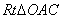 .
.
 ∴
∴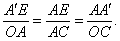 即
即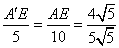 .
.
∴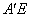 =4,AE=8.
=4,AE=8.
∴OE=AE-OA=3.
∴点A/的坐标为(﹣3,4).
当x=﹣3时,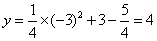 .
.
所以,点A/在该抛物线上
(3)存在.
理由:设直线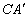 的解析式为y=kx+b,
的解析式为y=kx+b,
则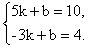 ,解得
,解得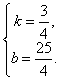
∴直线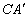 的解析式为
的解析式为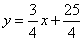 .
.
设点P的坐标为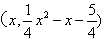 ,则点M为
,则点M为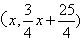 .
.
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴ 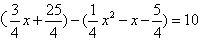 .
.
解得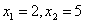 (不合题意,舍去)当x=2时,
(不合题意,舍去)当x=2时, .
.
∴当点P运动到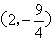 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.

练习册系列答案
相关题目
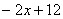 的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.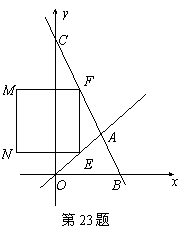 (4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.

 20° D.150°
20° D.150°
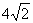 ,则a的值是
,则a的值是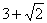 C.
C.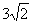

 D.
D.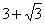
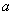 的说法中,错误的是( )
的说法中,错误的是( )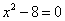 的解
的解  算术平方根 D. a满足不等式组
算术平方根 D. a满足不等式组
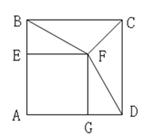
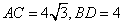 ,动点P在线段BD上从点B向点D运动,PP′⊥AB于点P′,四边形PFBG关于BD对称。四边形QEDH与四边形PFBG关于AC对称,设菱形ABCD被这两个四边形盖住部分的面积为
,动点P在线段BD上从点B向点D运动,PP′⊥AB于点P′,四边形PFBG关于BD对称。四边形QEDH与四边形PFBG关于AC对称,设菱形ABCD被这两个四边形盖住部分的面积为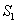 ,未盖住部分的面积为
,未盖住部分的面积为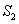 ,
,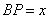 .
. )若
)若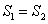 ,求x.
,求x.