题目内容
20. 将1,$\sqrt{2}$,$\sqrt{3}$三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(9,9)表示的两个数的积是( )
将1,$\sqrt{2}$,$\sqrt{3}$三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(9,9)表示的两个数的积是( )| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 1 |
分析 根据观察数列,可得,每三个数一循环,根据有序数对的表示方法,可得有序数对表示的数,根据是数的运算规律,可得答案.
解答 解:由题意可得:每三个数一循环,1、$\sqrt{2}$,$\sqrt{3}$,
(8,2)在数列中是第(1+7)×7÷2+2=30个,
30÷3=10,(8,2)表示的数正好是第10轮的最后一个,
即(8,2)表示的数是$\sqrt{3}$,
由题意可得:每三个数一循环,1、$\sqrt{2}$,$\sqrt{3}$,
(9,9)在数列中是第(1+8)×8÷2+9=45个,
45÷3=15,(9,9)表示的数正好是第15轮的最后一个,
即(9,9)表示的数是$\sqrt{3}$,
故(8,2)与(9,9)表示的两个数的积是:$\sqrt{3}$×$\sqrt{3}$=3.
故选:C.
点评 本题考查了数字的变化类以及实数运算,得出数字的变化规律是解题关键.

练习册系列答案
相关题目
10.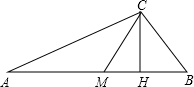 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )| A. | AB2=AC2+BC2 | B. | CH2=AH•HB | C. | CM=$\frac{1}{2}$AB | D. | CB=$\frac{1}{2}$AB |
 已知∠B=90°,AE,CH分别平分∠DAC,∠ACB.求∠H的度数.
已知∠B=90°,AE,CH分别平分∠DAC,∠ACB.求∠H的度数. 如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.
如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.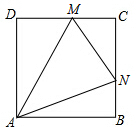 如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.
如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.