题目内容
5．求2（3+1）（32+1）（34+1）（38+1）…（364+1）的结果的个位数字．分析 由31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561…可知3n个位数字3、9、7、1四个数字一循环，利用平方差公式计算得到结果，再进一步判定即可．
解答 解：2（3+1）（32+1）（34+1）（36+1）…（366+1）
=（32-1）（32+1）（34+1）（36+1）…（366+1）
=（34-1）（34+1）（38+1）…（366+1）
=（38-1）（38+1）…（366+1）
=3132-1；
132÷4=33，
所以3132与34个位数字相同为1，
则结果的个位数字为1．
点评 此题考查了平方差公式和乘方末尾数字的规律，熟练掌握平方差公式是解本题的关键．
练习册系列答案
相关题目
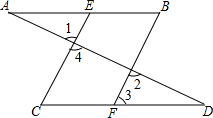如图，已知AD与AB，CD相交于A，D两点，EC，BF与AB，CD相交于点E，C，B，F，且∠1=∠2，∠B=∠C，
20．
将1，$\sqrt{2}$，$\sqrt{3}$三个数按图中方式排列，若规定（a，b）表示第a排第b列的数，则（8，2）与（9，9）表示的两个数的积是（ ）
将1，$\sqrt{2}$，$\sqrt{3}$三个数按图中方式排列，若规定（a，b）表示第a排第b列的数，则（8，2）与（9，9）表示的两个数的积是（ ）| A． | $\sqrt{6}$ | B． | $\sqrt{3}$ | C． | 3 | D． | 1 |
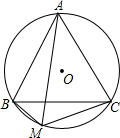已知：⊙O是△ABC的外接圆，点M为⊙O上一点．
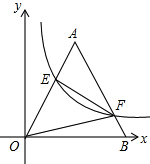若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA，AB分别相交于E，F两点，且EF⊥AE，则实数k的值为$\frac{36\sqrt{3}}{25}$．