题目内容
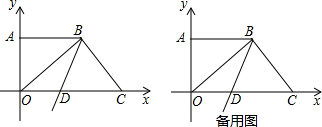
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO为梯形,C在x轴上,AB∥OC,OB⊥BC,点B的坐标是(
,
),点D为OC的中点.
(1)求点D的坐标;
(2)若点P从点O出发,以每秒4个单位长度的速度沿线段OB向终点B运动.过点P作OB的垂线,交x轴于点E,交射线BD于点F,设点P运动时间为t秒,EF的长为y,求y与t之间的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,连接CF,是否存在这样的t值,使∠ECF=
∠AOB?若存在,求出t的值;若不存在,请说明理由.
| 32 |
| 5 |
| 24 |
| 5 |
(1)求点D的坐标;
(2)若点P从点O出发,以每秒4个单位长度的速度沿线段OB向终点B运动.过点P作OB的垂线,交x轴于点E,交射线BD于点F,设点P运动时间为t秒,EF的长为y,求y与t之间的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,连接CF,是否存在这样的t值,使∠ECF=
| 1 |
| 2 |

考点:一次函数综合题
专题:
分析:(1)根据勾股定理,可得OB2,BC2,OC2,再根据勾股定理,可得关于a的方程,根据线段中点的性质,可得D点坐标;
(2)分类讨论:当0<t<1时,②当1<t<2时,根据像三角形的性质,可得y与t的关系式;
(3)根据余角的性质,可得∠AOB=∠C,根据角平分线的性质,可得FB与FE的关系,根据全等三角形的判定与性质,可得CE的长,根据相似三角形的性质,可得关于t的方程,根据解方程,可得答案.
(2)分类讨论:当0<t<1时,②当1<t<2时,根据像三角形的性质,可得y与t的关系式;
(3)根据余角的性质,可得∠AOB=∠C,根据角平分线的性质,可得FB与FE的关系,根据全等三角形的判定与性质,可得CE的长,根据相似三角形的性质,可得关于t的方程,根据解方程,可得答案.
解答:解:(1)如图1,做BE⊥OC于E点.
 ,
,
设C(a,0),由勾股定理,得
OB2=OE2+OB2=(
)2+(
)2,
BC2=CE2+BE2=(a-
)2+(
)2,
OC2=OB2+BC2,即(
)2+(
)2+(a-
)2+(
)2=a2,
化简,得
a=128,
解得a=10,即C(10,0);
由点D为OC的中点,得D(5,0);
(2)设E点坐标为(a,0),
①当0<t<1时,如图2:
 ,
,
由△OPE∽△OBC,得
=
,解得a=5t,
由△DEF∽△DCB,得
=
,即y=-6t+6,(0<t<1);
②当1<t<2时,如图3:

由△OPE∽△OBC,得
=
,解得a=5t,
由△DEF∽△DCB,得
=
,即y=6t-6,(1<t<2);
(3)存在这样的t值,使∠ECF=
∠AOB,理由如下:
如图4:

作FE⊥OC与E点,
由∠C+∠BOC=90°,∠BOC+∠AOB=90°,
∴∠AOB=∠C,
由∠ECF=
∠AOB,得∠ECF=
∠C,
∴FE=FB.
在Rt△FEC和RT△FBC中,
,
Rt△FEC≌RT△FBC(HL),
CE=BC=6(全等三角形的对应边相等).
OE=4,
由△OPE∽△OBC,得
=
,即
=
,
解得t=
.
 ,
,设C(a,0),由勾股定理,得
OB2=OE2+OB2=(
| 32 |
| 5 |
| 24 |
| 5 |
BC2=CE2+BE2=(a-
| 32 |
| 5 |
| 24 |
| 5 |
OC2=OB2+BC2,即(
| 32 |
| 5 |
| 24 |
| 5 |
| 32 |
| 5 |
| 24 |
| 5 |
化简,得
| 64 |
| 5 |
解得a=10,即C(10,0);
由点D为OC的中点,得D(5,0);
(2)设E点坐标为(a,0),
①当0<t<1时,如图2:
 ,
,由△OPE∽△OBC,得
| 4t |
| 8 |
| a |
| 10 |
由△DEF∽△DCB,得
| 5-5t |
| 10-5 |
| y |
| 6 |
②当1<t<2时,如图3:

由△OPE∽△OBC,得
| 4t |
| 8 |
| a |
| 10 |
由△DEF∽△DCB,得
| 5t-5 |
| 10-5 |
| y |
| 6 |
(3)存在这样的t值,使∠ECF=
| 1 |
| 2 |
如图4:

作FE⊥OC与E点,
由∠C+∠BOC=90°,∠BOC+∠AOB=90°,
∴∠AOB=∠C,
由∠ECF=
| 1 |
| 2 |
| 1 |
| 2 |
∴FE=FB.
在Rt△FEC和RT△FBC中,
|
Rt△FEC≌RT△FBC(HL),
CE=BC=6(全等三角形的对应边相等).
OE=4,
由△OPE∽△OBC,得
| OP |
| OB |
| OE |
| OC |
| 4t |
| 8 |
| 4 |
| 10 |
解得t=
| 4 |
| 5 |
点评:本题考查了一次函数的综合题,(1)利用了勾股定理,线段中点的性质;(2)利用了相似三角形的性质,分类讨论是解题关键;(3)利用了余角的性质,角平分线的性质,全等三角形的判定与性质,相似三角形的性质.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
以下事件中,必然发生的是( )
| A、打开电视机,正在播放体育节目 |
| B、正五边形的外角和为180° |
| C、a是实数,|a|≥0 |
| D、抛一次骰子,向上一面是5点 |
 如图,若y1≥y2,则x的取值范围是
如图,若y1≥y2,则x的取值范围是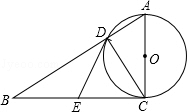 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,点E是边BC的中点. 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB,连接AF,BF. 如图,△ABC,AB=5,BC=4,AC=3.
如图,△ABC,AB=5,BC=4,AC=3.