题目内容
如图,在△ABC中,∠ABC=90°.AB=BC,A(-4,0),B(0,2)
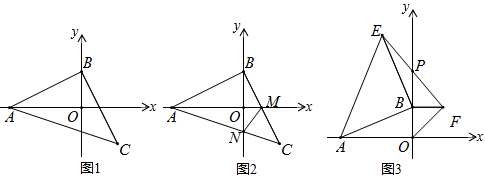
(1)如图1,求点C的坐标;
(2)如图2,BC交x轴于点M,AC交y轴于点N,且BM=CM,求证:∠AMB=∠CMN;
(3)如图3,若点A不动,点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、第二象限作等腰直角△BOF与等腰直角△ABE,连接EF交y轴于P点,问当点B在y轴正半轴上移动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出其长度.

(1)如图1,求点C的坐标;
(2)如图2,BC交x轴于点M,AC交y轴于点N,且BM=CM,求证:∠AMB=∠CMN;
(3)如图3,若点A不动,点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、第二象限作等腰直角△BOF与等腰直角△ABE,连接EF交y轴于P点,问当点B在y轴正半轴上移动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出其长度.
考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:(1)作CD⊥BO,易证△ABO≌△BCD,根据全等三角形对应边相等的性质即可解题;
(2)找到G点使得MG=MN,分别求得M,N的坐标,可以求得BG=CN,即可求得△CMN≌△BMG,根据全等三角形对应角相等即可解题;
(3)作EG⊥y轴,易证△BAO≌△EBG和△EGP≌△FBP,可得BG=AO和PB=PG,即可求得PB=
AO,即可解题.
(2)找到G点使得MG=MN,分别求得M,N的坐标,可以求得BG=CN,即可求得△CMN≌△BMG,根据全等三角形对应角相等即可解题;
(3)作EG⊥y轴,易证△BAO≌△EBG和△EGP≌△FBP,可得BG=AO和PB=PG,即可求得PB=
| 1 |
| 2 |
解答:解:(1)作CD⊥BO,
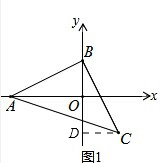
∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中,
,
∴△ABO≌△BCD(AAS),
∴BD=AO=4,CD=BO=2,
∴C点坐标(2,-2);
(2)找到G点使得MG=MN,
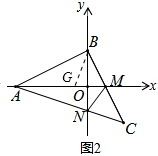
∵直线BC经过B(0,2),C(2,-2),设直线BC解析式为y=kx+b,
代入B、C得直线BC解析式为y=-2x+2,
∴M点坐标为(1,0)
∵直线AC经过A(-4,0),C(2,-2),设直线AC解析式为y=kx+b,
代入A、C得直线BC解析式为y=-
x-
,
∴N点坐标为(0,-
),
∴RT△OMN中,MN=
=
,
∵MG=MN,∴G点坐标为(-
,0)
∴GB=CN,
在△CMN和△BMG中,
,
∴△CMN≌△BMG(SSS),
∴∠AMB=∠CMN;
(3)作EG⊥y轴,
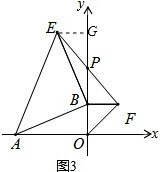
∵∠BAO+∠OBA=90°,∠OBA+∠EBG=90°,
∴∠BAO=∠EBG,
在△BAO和△EBG中,
,
∴△BAO≌△EBG(AAS),
∴BG=AO,EG=OB,
∵OB=BF,
∴BF=EG,
在△EGP和△FBP中,
,
∴△EGP≌△FBP(AAS),
∴PB=PG,
∴PB=
BG=
AO=2.

∵∠CBD+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠CBD=∠BAO,
在△ABO和△BCD中,
|
∴△ABO≌△BCD(AAS),
∴BD=AO=4,CD=BO=2,
∴C点坐标(2,-2);
(2)找到G点使得MG=MN,

∵直线BC经过B(0,2),C(2,-2),设直线BC解析式为y=kx+b,
代入B、C得直线BC解析式为y=-2x+2,
∴M点坐标为(1,0)
∵直线AC经过A(-4,0),C(2,-2),设直线AC解析式为y=kx+b,
代入A、C得直线BC解析式为y=-
| 1 |
| 3 |
| 4 |
| 3 |
∴N点坐标为(0,-
| 4 |
| 3 |
∴RT△OMN中,MN=
| OM2+ON2 |
| 5 |
| 3 |
∵MG=MN,∴G点坐标为(-
| 2 |
| 3 |
∴GB=CN,
在△CMN和△BMG中,
|
∴△CMN≌△BMG(SSS),
∴∠AMB=∠CMN;
(3)作EG⊥y轴,

∵∠BAO+∠OBA=90°,∠OBA+∠EBG=90°,
∴∠BAO=∠EBG,
在△BAO和△EBG中,
|
∴△BAO≌△EBG(AAS),
∴BG=AO,EG=OB,
∵OB=BF,
∴BF=EG,
在△EGP和△FBP中,
|
∴△EGP≌△FBP(AAS),
∴PB=PG,
∴PB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,熟练掌握三角形全等的证明是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列判断正确的有( )
①描述一组数据的平均数、方差只有一个;
②描述一组数据的中位数、极差只有一个;
③描述一组数据的众数只有一个;
④描述一组数据的平均数、中位数、众数都一定是这组数据中的数;
⑤一组数据中的一个数的大小发生了变化,一定会影响这组数据的平均数,众数和中位数.
①描述一组数据的平均数、方差只有一个;
②描述一组数据的中位数、极差只有一个;
③描述一组数据的众数只有一个;
④描述一组数据的平均数、中位数、众数都一定是这组数据中的数;
⑤一组数据中的一个数的大小发生了变化,一定会影响这组数据的平均数,众数和中位数.
| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,∠A=
∠B=
∠C,则此三角形是( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
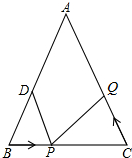 P从点B出发沿B-C-A以3厘米/秒的速度运动,点Q在从点C出发沿C-A-B运动,PQ两点同时运动,同时停止,运动时间为t秒.
P从点B出发沿B-C-A以3厘米/秒的速度运动,点Q在从点C出发沿C-A-B运动,PQ两点同时运动,同时停止,运动时间为t秒.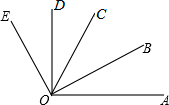 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线. 已知:如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,求证:BD=DE.
已知:如图,△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD,求证:BD=DE.