题目内容

已知等腰△ABC的一边长a=3，另两边长b、c恰好是关于x的方程x2-（k+2）x+2k=0的两个根，求△ABC的周长．
考点：等腰三角形的性质,解一元二次方程-因式分解法
专题：
分析：先利用因式分解法求出两根：x1=2，x2=k．先分类讨论：若a=3为底边；若a=3为腰，分别确定b，c的值，求出三角形的周长．
解答：解：x2-（k+2）x+2k=0
（x-2）（x-k）=0，
则x1=2，x2=k，
当b=c，
k=2，
则△ABC的周长=2+2+3=7，
当b=2，c=3或c=2，b=3
则k=3，
则△ABC的周长=2+3+3=8．
故△ABC的周长是7或8．
点评：本题考查了解一元二次方程-因式分解法：先把方程右边变形为0，然后把方程左边进行因式分解，这样把一元二次方程转化为两个一元一次方程，再解一次方程可得到一元二次方程的解．也考查了解等腰三角形的性质．
练习册系列答案
相关题目
计算：
2012
20132-20112
．
翻转类的计算问题在全国各地的中考试卷中出现的频率很大，因此小菲同学结合某市数学中考卷的倒数第二题对这类问题进行了专门的研究．你能和小菲一起解决下列各问题吗？（以下各问只要求写出必要的计算过程和简洁的文字说明即可．）
（1）如图①，小菲同学把一个边长为1的正三角形纸片（即△OAB）放在直线l1上，OA边与直线l1重合，然后将三角形纸片向右翻转一周回到初始位置，求顶点O所经过的路程；
（2）小菲进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l2上，OA边与直线l2重合，然后将正方形纸片向右翻转若干次．她提出了如下问题：
问题①：若正方形纸片OABC接上述方法翻转一周回到初始位置，求顶点O经过的路程；
问题②：正方形纸片OABC按上述方法经过
 
次旋转，顶点O经过的路程是
41+20
2
2
π．
（3）①小菲又进行了进一步的拓展研究，若把这个正三角形的一边OA与这个正方形的一边OA重合（如图3），然后让这个正三角形在正方形上翻转，直到正三角形第一次回到初始位置（即O点，A点，B点的相对位置和初始时一样），求顶点O所经过的总路程．
②若把边长为1的正方形OABC放在边长为1的正五边形OABCD上翻转（如图④），直到正方形第一次回到初始位置（即O点，A点，B点，C点的相对位置和初始时一样），求顶点O所经过的总路程．
如图，在△ABC中，∠ABC=90°．AB=BC，A（-4，0），B（0，2）

（1）如图1，求点C的坐标；
（2）如图2，BC交x轴于点M，AC交y轴于点N，且BM=CM，求证：∠AMB=∠CMN；
（3）如图3，若点A不动，点B在y轴的正半轴上运动时，分别以OB、AB为直角边在第一、第二象限作等腰直角△BOF与等腰直角△ABE，连接EF交y轴于P点，问当点B在y轴正半轴上移动时，BP的长度是否变化？若变化请说明理由，若不变化，请求出其长度．
下列说法错误的是（　　）
A、-xy的系数是-1
B、-
2
3
a2b3c是五次单项式
C、2x2-3xy-1是二次三项式
D、把多项式-2x2+3x3-1+x按x的降幂排列是3x3-2x2+x-1
判断
1
x
=2和|x|=2是不是一元一次方程？并说明理由．
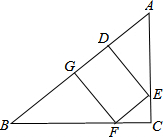如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，在线段AB上取一点D，过D作DE⊥AB交AC于E，过E作EF⊥DE交BC于F，过F作FG⊥EF交AB于G，得到矩形DEFG．
（1）设AD=x，用x表示DE、BG．
（2）设矩形DEFG的面积为y，当x取何值时，y最大，并求出最大值．
把ab=cd写成比例式，下列写法中不正确的是（　　）
A、
a
d
=
c
b
B、
a
c
=
d
b
C、
b
c
=
d
a
D、
a
c
=
b
d
已知2x+y=3x+2，试比较x和y的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网