题目内容
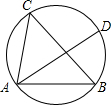 如图是一个圆形人工湖的示意图,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=60°,则这个人工湖的直径AD为( )
如图是一个圆形人工湖的示意图,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=60°,则这个人工湖的直径AD为( )A、
| ||||
B、
| ||||
C、100
| ||||
| D、150m |
考点:圆周角定理,解直角三角形
专题:应用题
分析:连接DB,由同弧所对的圆周角相等,可得∠ADB=∠ACB=60°,然后由直径所对的圆周角为90°,可得∠ABD=90°,最后由∠ADB的正弦即可求出AD的值.
解答:解:连接BD,
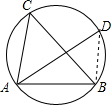
∵∠ADB=∠ACB,∠ACB=60°,
∴∠ADB=60°,
∵AD是直径,
∴∠ABD=90°,
在Rt△ADB中,
∵sin∠ADB=
,
∴sin60°=
,
∴AD=
=
m.
故选:B.

∵∠ADB=∠ACB,∠ACB=60°,
∴∠ADB=60°,
∵AD是直径,
∴∠ABD=90°,
在Rt△ADB中,
∵sin∠ADB=
| AB |
| AD |
∴sin60°=
| 100 |
| AD |
∴AD=
| 100 |
| sin60° |
200
| ||
| 3 |
故选:B.
点评:此题主要考查了圆周角定理,以及三角函数的应用,关键是证出∠ABD=90°,∠ADB=60°,在Rt△ADB中,由sin∠ADB,算出AD的长.

练习册系列答案
相关题目
 如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )
如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,将△ABC绕点B按顺时针方向转动一个角到△A′BC′的位置,使点A、B、C′在同一条直线上,则图中阴影部分的周长是( )A、4π+4
| ||
| B、4π | ||
C、2π+4
| ||
| D、2π |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=13cm,BC=12cm,求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=13cm,BC=12cm,求CD的长.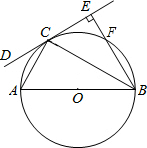 如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE.
如图,AB是⊙O的直径,C为⊙O上一点,过点B作经过点C的直线CD的垂线,垂足为E (即BE⊥CD),BE交⊙O于点F,且BC平分∠ABE. 如图,已知∠1+∠2=180°,∠B=∠3,∠ACB=60°,求∠AED的度数.
如图,已知∠1+∠2=180°,∠B=∠3,∠ACB=60°,求∠AED的度数.