Question

【题目】矩形纸片，，，在矩形边上有一点P，且，将矩形纸片折叠，使点C与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为_______.

Answer 1

【答案】或

【解析】

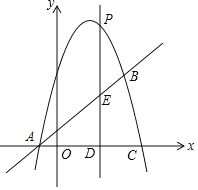
如图1，当点P在AD上时，由折叠的性质得到四边形PFCE是正方形，EF过点D，根据勾股定理即可得到结果；如图2当点P在AB上时，过E作EQ⊥BC于Q，根据勾股定理得到PC=，推出△CPB∽△EFQ，列比例式即可得到结果．

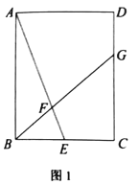
解：如图1，

当点P在AD上时，

∵AP=2，CD=AB=6，

∴PF=6，

∵EF垂直平分PC，

∴四边形PFCE是正方形，EF过点D，

∴EF=.

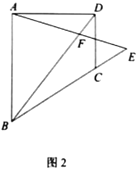
如图2，

当点P在AB上时，

过E作EQ⊥BC于Q，∵AP=2，AB=6，

∴BP=4，

∴PC=，

∵EF垂直平分PC，

∴∠1=∠2，

∵∠B=∠EQF，

∴△CPB∽△EFQ，

∴，

∴，

∴EF=,

综上所述：EF长为或.

故答案为：或