题目内容
8．分解因式：（x2-5x+4）（x2-x-2）-72．分析 先将题目中的式子化简，然后利用换元法可以对题目中的式子分解因式．
解答 解；（x2-5x+4）（x2-x-2）-72
=（x-4）（x-1）（x-2）（x+1）-72
=[（x-4）（x+1）][（x-1）（x-2）]-72
=（x2-3x-4）（x2-3x+2）-72
设x2-3x=t，
则（t-4）（t+2）-72
=t2-2t-80
=（t-10）（t+8）
=（x2-3x-10）（x2-3x+8）
=（x-5）（x+2）（x2-3x+8）．
点评 本题考查因式分解-十字相乘法，解题的关键是对题目中式子变形，利用换元法进行因式分解．
练习册系列答案
相关题目
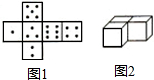有同样大小的三个立方体骰子，每个骰子的展开图如图1所示，如果把每个骰子点数是4的一面放在桌子上，那么其它五个可以看到的面上的数字的和是17，现在把三个骰子放在桌子上（如图2），凡是能看得到的点数之和最大是51，最小是26．
13．
某住宅小区六月份中1日至6日每天用水量变化情况如图所示，那么这6天的平均用水量是（ ）
某住宅小区六月份中1日至6日每天用水量变化情况如图所示，那么这6天的平均用水量是（ ）| A． | 30吨 | B． | 31吨 | C． | 32吨 | D． | 33吨 |