题目内容
15. 如图,C为线段AB上一点,D是线段AC的中点,E为线段CB的中点.
如图,C为线段AB上一点,D是线段AC的中点,E为线段CB的中点.(1)如果AC=6cm,BC=4cm,试求DE的长;
(2)如果AB=a,试探求DE的长度;
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,D,E分别为AC,BC的中点,你能猜想DE的长度吗?直接写出你的结论,不需要说明理由.
分析 (1)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(3)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案.
解答 解:(1)∵点D,E分别是AC,BC的中点,AC=6cm,BC=4cm,
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,CE=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2,
∴MN=CM+CN=3+2=5cm;
(2)∵点D,E分别是AC,BC的中点,
∴CD=$\frac{1}{2}$AC,CE=$\frac{1}{2}$BC,
∴DE=CD+CE=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$AB=$\frac{1}{2}$a(cm);
(3)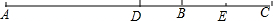 猜想:DE=$\frac{1}{2}$b,
猜想:DE=$\frac{1}{2}$b,
理由:∵点D,E分别是AC,BC的中点,AC=AB+BC
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$(AB+BC),CE=$\frac{1}{2}$BC,
∴DE=CD-CE=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC )=$\frac{1}{2}$b(cm).
点评 本题考查了两点间的距离,利用了线段中点的性质得出CM、CN的长,线段的和差得出答案.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.设关于x的方程ax2+(a+2)x+9a=0的两实根满足x1<1<x2.则a的取值范围是( )
| A. | -$\frac{2}{7}$<a<$\frac{2}{5}$ | B. | -$\frac{2}{11}$<a<0 | C. | -$\frac{2}{7}$<a<0 | D. | a>-$\frac{2}{11}$ |