��Ŀ����
����Ŀ���龳�۲�
������![]() ֽƬ�ضԽ���
ֽƬ�ضԽ���![]() �������õ�
�������õ�![]() ��
��![]() ����ͼ
����ͼ![]() ��ʾ����
��ʾ����![]() �Ķ���
�Ķ���![]() ���
���![]() �غϣ����Ƶ�
�غϣ����Ƶ�![]() ����ʱ�뷽����ת��ʹ��
����ʱ�뷽����ת��ʹ��![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ���ͼ
��ͬһ��ֱ���ϣ���ͼ![]() ��ʾ��
��ʾ��
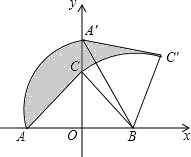
�۲�ͼ![]() ��֪����
��֪����![]() ��ȵ��߶���________��
��ȵ��߶���________��![]() ________�㣮
________�㣮

����̽��
��ͼ![]() ��
��![]() ��
�У�![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊֱ�Ƕ��㣬�ֱ���
Ϊֱ�Ƕ��㣬�ֱ���![]() ��
��![]() Ϊֱ�DZߣ���
Ϊֱ�DZߣ���![]() ��������
��������![]() �͵���
�͵���![]() ������
������![]() ��
��![]() ������
������![]() �Ĵ��ߣ�����ֱ�Ϊ
�Ĵ��ߣ�����ֱ�Ϊ![]() ��
��![]() ����̽��
����̽��![]() ��
��![]() ֮���������ϵ����֤����Ľ��ۣ�
֮���������ϵ����֤����Ľ��ۣ�
��չ����

��ͼ![]() ��
��![]() ��
�У�![]() �ڵ�
�ڵ�![]() ���ֱ���
���ֱ���![]() ��
��![]() Ϊһ����
Ϊһ����![]() ��������
��������![]() �;���
�;���![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����̽��
����̽��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
���𰸡���![]() ��
��![]() ����
����![]() �����ɼ���������
�����ɼ���������![]() �����ɼ�����.
�����ɼ�����.
��������
�ٹ۲�ͼ�μ��ɷ��֡�ABC�ա�AC��D�����ɽ��⣻
����֤��AEP�ա�BAG����AFQ�ա�CAG���������EP=AG��FQ=AG�����ɽ��⣻
�۹���E��EP��GA��FQ��GA������ֱ�ΪP��Q������ȫ�������ε��ж������ʼ��ɽ��⣮
�ٹ۲�ͼ�μ��ɷ���![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��![]() ��
��
�������£�
��![]() ��
��![]() ��
��
��![]() ��ͬ��
��ͬ��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ��![]() ��
��
��![]() ��
��
��![]() ��
��

���ɣ�����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�