题目内容
20.计算(1)(x+y)7÷(x+y)5•(x+y)3
(2)a•a2•a3+(-2a3)2-a8÷a2
(3)(y2)4•y-(-2y)3•y6
(4)${(\frac{1}{2})^{-1}}$+(π-2006)0-${(\frac{1}{3})^2}$
(5)${({-\frac{1}{2}})^{-2}}$+(π-3.14)0+(-0.2)2009×(-5)2010.
分析 (1)根据同底数幂的乘除法则进行计算即可;
(2)先算乘方,再算乘除,最后合并即可;
(3)先算乘方,再算乘法,最后合并即可;
(4)先根据零指数幂,负整数指数幂,有理数的乘方分别求出每一部分的值,再代入求出即可;
(5)先根据零指数幂,负整数指数幂,有理数的乘方分别求出每一部分的值,再代入求出即可.
解答 解:(1)(x+y)7÷(x+y)5•(x+y)3
=(x+y)7-5+3
=(x+y)5;
(2)a•a2•a3+(-2a3)2-a8÷a2
=a6+4a6-a6
=4a6;
(3)(y2)4•y-(-2y)3•y6
=y8•y+8y3•y6
=y9+8y9
=9y9;
(4)${(\frac{1}{2})^{-1}}$+(π-2006)0-${(\frac{1}{3})^2}$
=2+1-$\frac{1}{9}$
=2$\frac{8}{9}$;
(5)${({-\frac{1}{2}})^{-2}}$+(π-3.14)0+(-0.2)2009×(-5)2010
=4+1+[(-0.2)×(-5)]2009×(-5)
=5+12009×(-5)
=0.
点评 本题考查了有理数的混合运算和整式的混合运算的应用,能正确运用运算法则进行化简和计算是解此题的关键,注意运算顺序.

练习册系列答案
相关题目
10. 如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:
如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:
甲:AC、∠ACB; 乙:EF、DE、AD; 丙:AD、DE和∠DCB; 丁:CD、∠ABC、∠ADB.
其中能求得A、B两地距离的数据有( )
 如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:
如图,已知AE与BF相交于点D,AB⊥AE,垂足为点A,EF⊥AE,垂足为点E,点C在AD上,连接BC,要计算A、B两地的距离,甲、乙、丙、丁四组同学分别测量了部分线段的长度和角的度数,各组分别得到以下数据:甲:AC、∠ACB; 乙:EF、DE、AD; 丙:AD、DE和∠DCB; 丁:CD、∠ABC、∠ADB.
其中能求得A、B两地距离的数据有( )
| A. | 甲、乙两组 | B. | 丙、丁两组 | C. | 甲、乙、丙三组 | D. | 甲、乙、丁三组 |
5.下列计算正确的是( )
| A. | 3a3-a2=2a | B. | (2a-b)2=4a2-b2 | C. | (-2a2)3=-8a6 | D. | (-a)2÷a=-a |
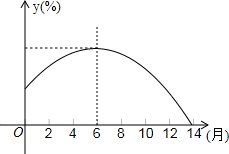 对某城市最近十几个月商品房价格涨幅情况进行调查,分析发现,与去年同期相比,房价涨幅y(%)与第x个月近似于二次函数y=-$\frac{1}{4}$x2+3x+7,如图所示,结合所学的知识,判断下列问题正确的个数为( )
对某城市最近十几个月商品房价格涨幅情况进行调查,分析发现,与去年同期相比,房价涨幅y(%)与第x个月近似于二次函数y=-$\frac{1}{4}$x2+3x+7,如图所示,结合所学的知识,判断下列问题正确的个数为( )