题目内容
11.不等式$\frac{x+1}{2}$>$\frac{2x+2}{3}$-1的所有正整数解的和为10.分析 先根据不等式的性质求出不等式的解集,再根据不等式的解集找出所有正整数解即可.
解答 解:去分母,得:3(x+1)>2(2x+2)-6,
去括号,得:3x+3>4x+4-6,
移项,得:3x-4x>4-6-3,
合并同类项,得:-x>-5,
系数化为1,得:x<5,
∴不等式所有正整数解得和为:1+2+3+4=10,
故答案为:10.
点评 本题考查了不等式的性质,解一元一次不等式,一元一次不等式的整数解的应用,解此题的关键是求出不等式的解集.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2.以下运算正确的是( )
| A. | $\sqrt{1.2}$是最简二次根式 | |
| B. | 三边长分别为4、5、6的三角形是直角三角形 | |
| C. | 直角三角形两直角边的和等于斜边的长 | |
| D. | 等腰直角三角形腰长为1,则斜边长为$\sqrt{2}$ |
3.若a>b,则下列式子正确的是( )
| A. | a-3>b-3 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | a-b<0 | D. | -3a>-3b |
20.下列多项式中能用平方差公式分解因式的是( )
| A. | a2+(-b)2 | B. | 3m2-12m | C. | -m2-n2 | D. | -x2+1 |
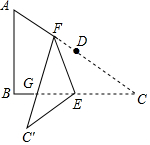 如图,在Rr△ABC中,∠B=90°,AB=3,BC=4,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C′EF,C′F交BC于点G.当△CFG与△ABC相似时,CF的长为4或2.8.
如图,在Rr△ABC中,∠B=90°,AB=3,BC=4,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C′EF,C′F交BC于点G.当△CFG与△ABC相似时,CF的长为4或2.8. 如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.