题目内容
16. 某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由.
分析 (1)设饲养室宽为x(m),则长为(60-4x)m,根据长方形面积公式即可得,由墙可用长≤20m可得x的范围;
(2)令y=210求出x,根据(1)中x的范围即可判断.
解答 解:(1)设饲养室宽为x(m),则长为(60-4x)m,
∴y=x(60-4x)=-4x2+60x,
∵0<60-4x≤20,
∴10≤x<15;
(2)不能,理由如下:
当y=210时,-4x2+60x=210,
解得:x=$\frac{15+\sqrt{15}}{2}$或x=$\frac{15-\sqrt{15}}{2}$,
∵x=$\frac{15+\sqrt{15}}{2}$<10,且x=$\frac{15-\sqrt{15}}{2}$<10,
∴不能.
点评 本题主要考查二次函数的应用,解题的关键是将实际问题转化为数学问题以后,准确列出二次函数关系式,正确运用二次函数的有关性质来解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
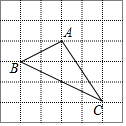 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$. 如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.
如图,菱形ABCD中,AB=4,∠ABC=60°,对称中心为P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=60°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1.