题目内容
2. 如图所示,已知直线AB∥CD,FH平分∠DFE,FG⊥FH,∠AEF=50°,则∠GFC=65度.
如图所示,已知直线AB∥CD,FH平分∠DFE,FG⊥FH,∠AEF=50°,则∠GFC=65度.
分析 先根据平行线的性质求出∠DFE及∠EFC的度数,再由角平分线的性质得出∠EFH的度数,根据余角的定义求出∠EFG的度数,进而可得出结论.
解答 解:∵直线AB∥CD,∠AEF=50°,
∴∠DFE=50°,∠EFC=180°-50°=130°.
∵FH平分∠DFE,
∴∠EFH=$\frac{1}{2}$∠DFE=25°.
∵FG⊥FH,
∴∠EFG=90°-25°=65°,
∴∠GFC=∠EFC-∠EFG=130°-65°=65°.
故答案为:65.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等,同旁内角互补.

练习册系列答案
相关题目
17. △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
 △ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )
△ABO与△A1B1O在平面直角坐标系中的位置如图所示,它们关于点O成中心对称,其中点A(5,2),则点A1的坐标是( )| A. | (5,-2) | B. | (-5,-2) | C. | (-2,-5) | D. | (-2,5) |
7.点A在点O的南偏东30°,点B在点O的北偏西70°,则OA,OB这两条射线构成的角等于( )
| A. | 140° | B. | 100° | C. | 80° | D. | 40° |
11.(-1)2016的相反数是( )
| A. | 1 | B. | -1 | C. | 2016 | D. | -2016 |
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米. 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.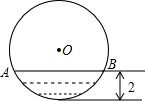 如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4$\sqrt{3}$,求⊙O的半径.
如图,水平放置的圆柱形排水管的截面为⊙O,有水部分弓形的高为2,弦AB=4$\sqrt{3}$,求⊙O的半径.