Question

12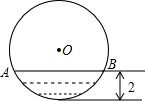．如图，水平放置的圆柱形排水管的截面为⊙O，有水部分弓形的高为2，弦AB=4$\sqrt{3}$，求⊙O的半径．

Answer 1

分析 首先过点O作OC⊥AB于点D，交$\widehat{AB}$于点C，连接OB，设⊙O的半径为r，则OD=r-2，由垂径定理得BD=$\frac{1}{2}$AB，再利用勾股定理可得结果．

解答 解：过点O作OC⊥AB于点D，交$\widehat{AB}$于点C，连接OB，
设⊙O的半径为r，则OD=r-2，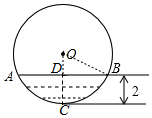
∵OC⊥AB，
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$，
在Rt△BOD中，
∵OD²+BD²=OB²，即（r-2）²+（2$\sqrt{3}$）²=r²，
解得r=4．

点评 本题主要考查了垂径定理和勾股定理，作出恰当的辅助线，利用定理是解答此题的关键．