题目内容
6.已知实数x、y、z满足$\left\{\begin{array}{l}{4x-3y=0}\\{3y-2z=0}\end{array}\right.$,试求$\frac{x+2y-z}{2x-y+z}$的值.分析 先根据x、y、z满足$\left\{\begin{array}{l}{4x-3y=0}\\{3y-2z=0}\end{array}\right.$,求出:x=$\frac{3}{4}$y,z=$\frac{3}{2}$y,然后代入求值即可.
解答 解:∵实数x、y、z满足$\left\{\begin{array}{l}{4x-3y=0}\\{3y-2z=0}\end{array}\right.$,
∴x=$\frac{3}{4}$y,z=$\frac{3}{2}$y,
将x=$\frac{3}{4}$y,z=$\frac{3}{2}$y代入$\frac{x+2y-z}{2x-y+z}$可得:
$\frac{x+2y-z}{2x-y+z}$
=$\frac{\frac{3}{4}y+2y-\frac{3}{2}y}{2×\frac{3}{4}y-y+\frac{3}{2}y}$
=$\frac{5}{8}$.
点评 本题考查了分式的值,解答本题的关键在于根据x、y、z满足$\left\{\begin{array}{l}{4x-3y=0}\\{3y-2z=0}\end{array}\right.$,求出:x=$\frac{3}{4}$y,z=$\frac{3}{2}$y,然后代入求值.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
11.$\frac{1}{3}$是( )
| A. | 无理数 | B. | 有理数 | C. | 整数 | D. | 有限小数 |
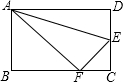 如图,折叠矩形ABCD的一边AD,使点D落在BC边F处,已知折痕AE=5$\sqrt{5}$,且tan∠EFC=$\frac{3}{4}$.
如图,折叠矩形ABCD的一边AD,使点D落在BC边F处,已知折痕AE=5$\sqrt{5}$,且tan∠EFC=$\frac{3}{4}$.