一次函数y=-x+1与y=x-7的图象的交点坐标为．题目和参考答案——青夏教育精英家教网—

题目内容

11．一次函数y=-x+1与y=x-7的图象的交点坐标为（4，-3）．

分析根据函数图象交点坐标为两函数解析式组成的方程组的解，通过解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=x-7}\end{array}\right.$即可得到两函数图象的交点坐标．

解答解：解方程组$\left\{\begin{array}{l}{y=-x+1}\\{y=x-7}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$，
所以一次函数y=-x+1与y=x-7的图象的交点坐标为（4，-3）．
故答案为（4，-3）．

点评本题考查了一次函数与二元一次方程：函数图象交点坐标为两函数解析式组成的方程组的解．

练习册系列答案

北教传媒实战中考系列答案

宏翔文化寒假一本通期末加寒假加预习系列答案

寒假衔接班寒假提优20天江苏人民出版社系列答案

x²+y+y²

19．在△ABC中，若cosA=$\frac{{\sqrt{3}}}{2}$，tanB=$\sqrt{3}$，这个三角形一定是（　　）

6．

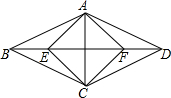如图，菱形ABCD中，点E、F在对角线BD上，BE=DF=$\frac{1}{4}$BD，若四边形AECF为正方形，则tan∠ABE=$\frac{1}{2}$．

16．2008年5月12日14时28分，我国四川省汶川地区发生里氏8.0级强烈地震，给当地人民造成巨大经济损失．齐村中学积极组织捐款支援灾区，八（1）班55名同学共捐款274元，捐款情况如下表，表中捐款2元和5元的人数不小心被墨水污染已看不清楚，请你帮忙确定表中数据，并说明理由．

捐款（元）	1	2	5	10
人数	6			7

3．工商部门的执法人员为检查某种品牌的1万瓶矿泉水是否符合食品卫生标准，随机抽取了100瓶样品进行化验，在这次调查中，工商部门的执法人员采取了哪种调查是抽样调查．调查中考察对象的总体是10000瓶矿泉水的卫生情况的全体，个体是每瓶矿泉水的卫生情况，样本是100矿泉水的卫生情况．

20．方程${x}^{2}-4x+3=0}\\{{x}^{2}-16=0}\end{array}\right.$的解是x₁=1，x₂=3．

1．计算或化简：
（1）（-3）+（-2）；
（2）（-8）-（+6）；
（3）$-0.5-（-3\frac{1}{4}）+2.75-（+7\frac{1}{2}）$；
（4）$1÷（{-\frac{2}{7}}）×\frac{1}{7}$；
（5）（-48）÷8-（-25）×（-4）+6；
（6）$（{\frac{3}{8}-\frac{1}{6}-\frac{3}{4}}）×24$；
（7）2$\frac{1}{5}$×（$\frac{1}{3}$-$\frac{1}{2}$）×$\frac{3}{11}$÷1$\frac{1}{4}$
（8）（-4）×（-2$\frac{1}{7}$）+（-8）×（-214）+12×（-2-9）

试题分类