Question

如图，在△ABC中，AD为角平分线，CE⊥AD，F为BC中点．
求证：EF=（AB-AC）．

 

 

Answer 1

证明：如图，延长CE交AB于G，
∵AD为角平分线，
∴∠EAG=∠EAC，
∵CE⊥AD，
∴∠AEG=∠AEC=90°，
在△AGE和△ACE中，

∠EAG＝∠EAC, AE＝AE, ∠AEG＝∠AEC＝90°，
∴△AGE≌△ACE（ASA），
∴AG=AC，CE=GE，
又∵F为BC中点，
∴EF是△BCG的中位线，
∴EF=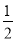BG=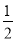（AB-AG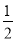）=（AB-AC），
即EF=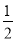（AB-AC）．

 

【解析】

延长CE交AB于G，利用“角边角”证明△AGE和△ACE全等，根据全等三角形对应边相等可得AG=AC，CE=GE，然后求出EF是△BCG的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半证明即可．