题目内容
8.阅读下列解题过程,并解决问题:已知m2+2m+n2-6n+10=0,求m、n的值
解:把原式整理,得(m+1)2+(n-3)2=0
因为(m+1)2≥0,(n-3)2≥0,所以m+1=0,n-3=0,即m=-1,n=3.
利用以上解法.解下列问题:
已知x2+y2-x+4y+$\frac{17}{4}$=0,求x和y的值.
分析 将已知等式左边$\frac{17}{4}$变形为4+$\frac{1}{4}$,重新结合并利用完全平方公式变形,根据两非负数之和为0,两非负数分别为0求出x与y的值.
解答 解:x2+y2-x+4y+$\frac{17}{4}$=0变形得,x2-x+$\frac{1}{4}$+y2+4y+4=0,
∴${(x-\frac{1}{2})}^{2}$+(y+2)2=0,
∴x-$\frac{1}{2}$=0且y+2=0,
∴x=$\frac{1}{2}$,y=-2.
点评 此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18.不等式3x-1≤2(x+2)的正整数解有几个( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.若(x+a)(x-b)=x2+mx+n,则m,n的值分别是( )
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
18. 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BAF=60°,则∠DAE=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
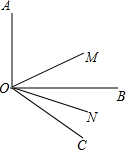 如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.
如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.