题目内容
3.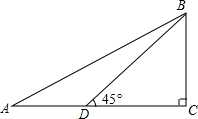 如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=$10\sqrt{2}$,AB=20,则∠A的度数是30°.
如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=$10\sqrt{2}$,AB=20,则∠A的度数是30°.
分析 先在Rt△ADC中利用正弦的定义可计算出BC=10$\sqrt{2}$×sin45°=10,然后在Rt△ABC中,利用正弦定义得到sin∠A=$\frac{BC}{AB}$=$\frac{1}{2}$,再利用特殊角的三角函数值即可得到∠A的度数.
解答 解:在Rt△ADC中,∵sin∠BDC=$\frac{BC}{BD}$,
∴BC=10$\sqrt{2}$×sin45°=10$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=10,
在Rt△ABC中,∵sin∠A=$\frac{BC}{AB}$=$\frac{10}{20}$=$\frac{1}{2}$,
∴∠A=30°.
故答案为30°.
点评 本题考查了解直角三角形:在直角三角形中,利用勾股定理、三角形内角和和三角函数,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
18.某种原子的直径是2×10-3纳米,把这个数化为小数是( )纳米.
| A. | 0.002 | B. | -0.002 | C. | 2000 | D. | 200 |
8.三角形A′B′C′是由三角形ABC平移得到的,点A(-1,-4)的对应点为A′(1,-1),则点B(1,1)的对应点B′、点C(-1,4)的对应点C′的坐标分别为( )
| A. | (2,2)(3,4) | B. | (3,4)(1,7) | C. | (-2,2)(1,7) | D. | (3,4)(2,-2) |
15. 如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
 如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )
如图,平行四边形ABCD中,BD=CD,∠C=70°,AE⊥BD于E,则∠DAE等于( )| A. | 10° | B. | 20° | C. | 25° | D. | 30° |
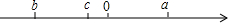 已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.
已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.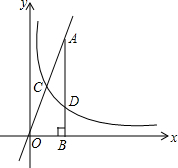 如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.