题目内容
11.抛物线y=x2-2x-1关于点(2,3)对称的解析式为y=-x2+6x-1.分析 先利用配方法得到抛物线y=x2-2x-1的顶点坐标为(1,-2),再找出点(1,-2)关于点(2,3)对称的对应点的坐标为(3,8),然后根据顶点式写出对称后的抛物线解析式.
解答 解:y=x2-2x-1=(x-1)2-2,抛物线y=x2-2x-1的顶点坐标为(1,-2),点(1,-2)关于点(2,3)对称的对应点的坐标为(3,8),由于对称后抛物线开口相反,所以对称后的抛物线解析式为y=-(x-3)2+8,即y=-x2+6x-1.
故答案为y=-x2+6x-1.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 如图,⊙O的半径为1,AB是⊙O的一条弦,AB=$\sqrt{3}$,则弦AB所对的圆周角的度数为( )
如图,⊙O的半径为1,AB是⊙O的一条弦,AB=$\sqrt{3}$,则弦AB所对的圆周角的度数为( )
 如图,⊙O的半径为1,AB是⊙O的一条弦,AB=$\sqrt{3}$,则弦AB所对的圆周角的度数为( )
如图,⊙O的半径为1,AB是⊙O的一条弦,AB=$\sqrt{3}$,则弦AB所对的圆周角的度数为( )| A. | 30° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
6.一次函数y=kx+b,当-3≤x≤l时,y的最小值和最大值分别为l和9,则k+b的值为( )
| A. | 9 | B. | 1 | C. | 1或9 | D. | -5 |

 如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为60°.
如图,AB、CD是⊙O的两条弦,连接AD、BC.若∠BAD=60°,则∠BCD的度数为60°.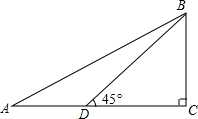 如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=$10\sqrt{2}$,AB=20,则∠A的度数是30°.
如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=$10\sqrt{2}$,AB=20,则∠A的度数是30°.