题目内容
如图，抛物线y=x2﹣2x﹣3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．
（1）求A、B两点的坐标及直线AC的函数表达式；
（2）P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值．
【考点】二次函数综合题．
【专题】压轴题；动点型．
【分析】（1）令y=0，解x2﹣2x﹣3=0，可得AB的坐标；将C的横坐标代入，易得其纵坐标，结合A的坐标，可ACC的方程；
（2）设出P点的横坐标，表示出P、E的坐标，可得PE长度的表达式，进而根据x的取值范围可得线段PE长度的最大值．
【解答】解：（1）令y=0，解得x1=﹣1或x2=3，
∴A（﹣1，0）B（3，0）；
将C点的横坐标x=2代入y=x2﹣2x﹣3
得y=﹣3，
∴C（2，﹣3），
设直线AC的解析式是y=kx+b，
把A（﹣1，0），C（2，﹣3）代入得：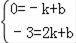
，
解得：k=﹣1，b=﹣1，
∴直线AC的函数解析式是y=﹣x﹣1；
（2）设P点的横坐标为x（﹣1≤x≤2）（注：x的范围不写不扣分）
则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3）
∵P点在E点的上方，PE=（﹣x﹣1）﹣（x2﹣2x﹣3）=﹣x2+x+2=﹣（x﹣
）2+
，
∴当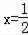
时，PE的最大值=．
．用放大镜观察蚂蚁的触角
③y=|x-3④y2=8x.其中y是x的函数的是