题目内容
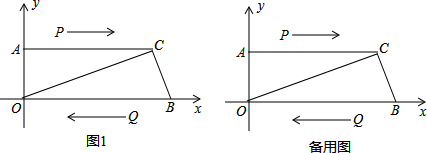
如图,平面直角坐标系xOy中,A(0,12),B(40,0),C(36,12),点P从点A出发,以1个单位/s的速度向点C运动;点Q从B同时出发,以2个单位/s的速度向点O运动,规定其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为ts.
(1)求过O,C,B三点的抛物线解析式;
(2)求证:△OCB为直角三角形;
(3)t为何值时,PQ=BC;
(4)在(1)中的抛物线上,是否存在点M,使以O,M,P,Q为顶点的四边形为平行四边形?若存在,直接写出此时t的值和M点的坐标;若不存在,请说明理由.
(1)求过O,C,B三点的抛物线解析式;
(2)求证:△OCB为直角三角形;
(3)t为何值时,PQ=BC;
(4)在(1)中的抛物线上,是否存在点M,使以O,M,P,Q为顶点的四边形为平行四边形?若存在,直接写出此时t的值和M点的坐标;若不存在,请说明理由.

考点:二次函数综合题,待定系数法求二次函数解析式,全等三角形的判定与性质,勾股定理,勾股定理的逆定理,平行四边形的性质
专题:压轴题
分析:(1)用待定系数法就可求出二次函数的解析式.
(2)过点C作CH⊥OB,垂足为H,运用勾股定理及其逆定理就可解决问题.
(3)由PQ=BC可分四边形PCBQ是平行四边形和等腰梯形两种情况进行讨论,就可以解决问题.
(4)分别以PQ为平行四边形的边和对角线进行讨论,就可解决问题.
(2)过点C作CH⊥OB,垂足为H,运用勾股定理及其逆定理就可解决问题.
(3)由PQ=BC可分四边形PCBQ是平行四边形和等腰梯形两种情况进行讨论,就可以解决问题.
(4)分别以PQ为平行四边形的边和对角线进行讨论,就可解决问题.
解答:解:(1)如图1,

由题可设y=ax(x-40),
∵点C(36,12)在抛物线y=ax(x-40)上,
∴a×36×(36-40)=12.
解得:a=-
.
∴y=-
x(x-40)=-
x2+
.
∴过O,C,B三点的抛物线的解析式为y=-
x2+
.
(2)证明:过点C作CH⊥OB,垂足为H,如图2,

∵点C坐标为(36,12),点B的坐标为(40,0),
∴OH=36,CH=12,OB=40.
∴OC2=OH2+CH2=362+122=1440,BC2=CH2+BH2=122+(40-36)2=160.
∴OC2+BC2=1600=OB2.
∴∠OCB=90°.
∴△OCB是直角三角形.
(3)①若四边形PCBQ是平行四边形,如图3,

则有PC=BQ.
∵AP=t,BQ=2t,AC=36,OB=40,
∴36-t=2t.
解得:t=12.
②若四边形PCBQ是等腰梯形,
过点P作PG⊥OB,垂足为G,如图4,

∵四边形PCBQ是等腰梯形,
∴PQ=CB,∠PQG=∠CBH.
在Rt△PGQ和Rt△CHB中,
∴Rt△PGQ≌Rt△CHB(AAS)
∴GQ=BH,PG=CH.
∵∠PGH=∠CHB=90°.
∴PG∥CH.
∴四边形PCHG是平行四边形.
∴PC=GH.
∴36-t=2t-2×4.
解得:t=
.
综上所述:当t为12秒或
秒时,PQ=BC
(4)①PQ为平行四边形的一条边,
Ⅰ.若四边形OPQM是平行四边形,如图5①,

过点P作PR⊥OB,垂足为R,过点M作MS⊥OB,垂足为S,
∵四边形OPQM是平行四边形,
∴PQ∥OM,PQ=OM.
∴∠MOQ=∠PQO.
∴∠SOM=∠RQP.
在△OSM和△QRP中,
,
∴△OSM≌△QRP(AAS).
∴SM=RP,OS=QR.
∵RP=12,
∴SM=12.
∴yM=-12.
∴-
x2+
=-12.
解得:x1=20+4
(舍去),x2=20-4
.
此时点M的坐标为(20-4
,-12),
QR=OS=4
-20,
OQ=OR-QR=AP-QR=t-(4
-20)=40-2t,
解得:t=
.
Ⅱ.若四边形OQPM是平行四边形,如图5②,

则有PM=OQ.
当y=12时,-
x2+
=12,
解得:x1=4,x2=36(舍去).
此时点M的坐标为(4,12),
PM=t-4,OQ=40-2t,
则有t-4=40-2t.
解得:t=
.
②PQ为平行四边形的一条对角线,如图6,

则四边形OPMQ是平行四边形.
∴PM∥OQ,PM=OQ.
∵点M既在PC上,又在抛物线上,
∴点M与点C重合,即点M的坐标为(36,12),
由PM=OQ得36-t=40-2t,
解得:t=4.
综上所述:当t=
时,M(20-4
,-12);当t=
时,M(4,12);当t=4时,M(36,12).

由题可设y=ax(x-40),
∵点C(36,12)在抛物线y=ax(x-40)上,
∴a×36×(36-40)=12.
解得:a=-
| 1 |
| 12 |
∴y=-
| 1 |
| 12 |
| 1 |
| 12 |
| 10x |
| 3 |
∴过O,C,B三点的抛物线的解析式为y=-
| 1 |
| 12 |
| 10x |
| 3 |
(2)证明:过点C作CH⊥OB,垂足为H,如图2,

∵点C坐标为(36,12),点B的坐标为(40,0),
∴OH=36,CH=12,OB=40.
∴OC2=OH2+CH2=362+122=1440,BC2=CH2+BH2=122+(40-36)2=160.
∴OC2+BC2=1600=OB2.
∴∠OCB=90°.
∴△OCB是直角三角形.
(3)①若四边形PCBQ是平行四边形,如图3,

则有PC=BQ.
∵AP=t,BQ=2t,AC=36,OB=40,
∴36-t=2t.
解得:t=12.
②若四边形PCBQ是等腰梯形,
过点P作PG⊥OB,垂足为G,如图4,

∵四边形PCBQ是等腰梯形,
∴PQ=CB,∠PQG=∠CBH.
在Rt△PGQ和Rt△CHB中,
|
∴Rt△PGQ≌Rt△CHB(AAS)
∴GQ=BH,PG=CH.
∵∠PGH=∠CHB=90°.
∴PG∥CH.
∴四边形PCHG是平行四边形.
∴PC=GH.
∴36-t=2t-2×4.
解得:t=
| 44 |
| 3 |
综上所述:当t为12秒或
| 44 |
| 3 |
(4)①PQ为平行四边形的一条边,
Ⅰ.若四边形OPQM是平行四边形,如图5①,

过点P作PR⊥OB,垂足为R,过点M作MS⊥OB,垂足为S,
∵四边形OPQM是平行四边形,
∴PQ∥OM,PQ=OM.
∴∠MOQ=∠PQO.
∴∠SOM=∠RQP.
在△OSM和△QRP中,
|
∴△OSM≌△QRP(AAS).
∴SM=RP,OS=QR.
∵RP=12,
∴SM=12.
∴yM=-12.
∴-
| 1 |
| 12 |
| 10x |
| 3 |
解得:x1=20+4
| 34 |
| 34 |
此时点M的坐标为(20-4
| 34 |
QR=OS=4
| 34 |
OQ=OR-QR=AP-QR=t-(4
| 34 |
解得:t=
20+4
| ||
| 3 |
Ⅱ.若四边形OQPM是平行四边形,如图5②,

则有PM=OQ.
当y=12时,-
| 1 |
| 12 |
| 10x |
| 3 |
解得:x1=4,x2=36(舍去).
此时点M的坐标为(4,12),
PM=t-4,OQ=40-2t,
则有t-4=40-2t.
解得:t=
| 44 |
| 3 |
②PQ为平行四边形的一条对角线,如图6,

则四边形OPMQ是平行四边形.
∴PM∥OQ,PM=OQ.
∵点M既在PC上,又在抛物线上,
∴点M与点C重合,即点M的坐标为(36,12),
由PM=OQ得36-t=40-2t,
解得:t=4.
综上所述:当t=
20+4
| ||
| 3 |
| 34 |
| 44 |
| 3 |
点评:本题考查了用待定系数法求二次函数的解析式、平行四边形的性质、等腰梯形的性质、全等三角形的判定与性质、勾股定理及其逆定理等知识,有一定的综合性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
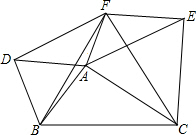 如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF.
如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF.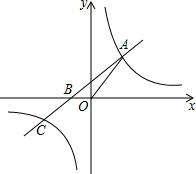 如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.
如图,直线y=kx+2k(k≠0)与x轴交于点B,与双曲线y=(m+5)x2m+1交于点A、C,其中点A在第一象限,点C在第三象限.