题目内容
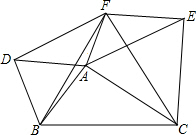 如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF.
如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE,等边△BCF.(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需要证明)
①当∠A=
②当△ABC满足
考点:菱形的判定,全等三角形的判定与性质,等边三角形的性质,平行四边形的判定,矩形的判定
专题:
分析:(1)根据等边三角形的性质得出AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,求出∠BCA=∠FCE,证△BCA≌△FCE,推出EF=BA=AD,同理DF=AC=AE,即可推出答案;
(2)①求出∠DAE的度数,根据矩形的判定推出即可;
②求出AD=AE,根据菱形的判定推出即可.
(2)①求出∠DAE的度数,根据矩形的判定推出即可;
②求出AD=AE,根据菱形的判定推出即可.
解答:(1)证明:∵△ABD、△BCE、△ACE是等边三角形,
∴AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,
∴∠BCA=∠FCE=60°-∠ACF,
在△BCA和△FCE中,
,
∴△BCA≌△FCE(SAS),
∴EF=BA=AD,
同理DF=AC=AE,
∴四边形DAEF是平行四边形;
(2)解:①当∠A=150°时,四边形DAEF是矩形,
理由是:∵△ABD、△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°-60°-60°-150°=90°,
∵四边形DAEF是平行四边形,
∴四边形DAEF是矩形,
故答案为:=150°;
②当△ABC满足AB=AC≠BC时,四边形DAEF是菱形,
理由是:由(1)知:EF=BA=AD,DF=AC=AE,
∵AB=AC,
∴AD=AE,
∵四边形DAEF是平行四边形,
∴四边形DAEF是菱形,
故答案为:AB=AC≠BC.
∴AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,
∴∠BCA=∠FCE=60°-∠ACF,
在△BCA和△FCE中,
|
∴△BCA≌△FCE(SAS),
∴EF=BA=AD,
同理DF=AC=AE,
∴四边形DAEF是平行四边形;
(2)解:①当∠A=150°时,四边形DAEF是矩形,
理由是:∵△ABD、△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°-60°-60°-150°=90°,
∵四边形DAEF是平行四边形,
∴四边形DAEF是矩形,
故答案为:=150°;
②当△ABC满足AB=AC≠BC时,四边形DAEF是菱形,
理由是:由(1)知:EF=BA=AD,DF=AC=AE,
∵AB=AC,
∴AD=AE,
∵四边形DAEF是平行四边形,
∴四边形DAEF是菱形,
故答案为:AB=AC≠BC.
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,平行四边形的判定,菱形的判定,矩形的判定的应用,解此题的关键是求出EF=BA=AD,DF=AC=AE,主要考查了学生的推理能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
一个不透明的袋中有形状和大小完全一样的8个小球,其中4个红色,2个黄色,2个白色,从袋中任意地同时摸出3个球,能摸到红球、黄球、蓝球的这件事件( )
| A、可能发生 | B、不可能发生 |
| C、很可能发生 | D、必然发生 |
 如图,四边形ABCD是菱形,对角线AC和BD相交于O点,DH垂直且平分AB,BD=8cm,求:DH,AC的长和菱形的面积.
如图,四边形ABCD是菱形,对角线AC和BD相交于O点,DH垂直且平分AB,BD=8cm,求:DH,AC的长和菱形的面积.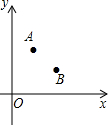 在平面直角坐标系xOy中,点A(1,2),B(2,1),C(4,3),
在平面直角坐标系xOy中,点A(1,2),B(2,1),C(4,3),