Question

在△ABC中，AD为BC边上的中线，若AB=6，AC=8，且AD为整数，求AD的长．

Answer 1

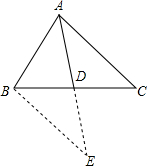解：如图，延长AD至E，使DE=AD，连接BE，
∵AD为BC边上的中线，
∴BD=CD，
在△ACD和△EBD中，
∵，
∴△ACD≌△EBD（SAS），
∴BE=AC，
∵AB=6，AC=8，
8-6=2，8+6=14，
∴2＜AE＜14，
∴1＜AD＜7，
∵AD为整数，
∴AD的长为：2或3或4或5或6．
故答案为：2或3或4或5或6．
分析：延长AD至E，使DE=AD，连接BE，利用“边角边”证明△ACD和△EBD全等，根据全等三角形对应边相等可得BE=AC，再利用三角形的三边关系求出AE的取值范围，从而得到AD的范围，再根据AD为整数即可得解．
点评：本题考查了全等三角形的判定与性质，三角形的任意两边之和大于第三边，两边之差小于第三边，“遇中线加倍延”作出辅助线，构造出全等三角形是解题的关键．